Funckja wymierna monotonicznosc Funckjawymierna: Dzień dobry . Jeśli mam funkcje wymierna to czy montonicznosc musze zapisać np ze funkcja jest malejąca w przedziałach (−nieskończoność, 0) i (0, nieskończoność). Czy mogę napisać, że funkcja jest malejąca dla x należących do R bez 0?

Funckjawymierna: Czy ten drugi zapisa sugeruje tylko, że funkcja jest ciągła, tylko 0 jakby nie należy do dziedziny? Nie wiem czy jest zrozumiałe to co pisze. Chodzi mi o to, że 0 byłoby po prostu z otwartym koleczkiem

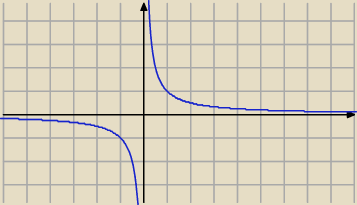
Saizou : Nie możesz, bo to by oznaczało, że w całej dziedzinie funkcja maleje, łatwo podać kontrprzykład dla R\{0}, aby funkcja była rosnąca, rozważ funkcję f(x)=1/x

Funckjawymierna: Czyli chodzi o to, że np.: f(−1) = −1 f(1) = 1 i to mogłoby wskazywać na to, że funkcja jest rosnąca? Dobrze zrozumiałam?

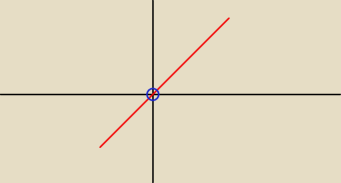
Funckjawymierna: A gdybym miała taki wykres, to mogę zapisać monotoniczność na 2 sposoby? 1) funkcja rosnąca dla x należących od (−nieskończoności,0) i (0, nieskończoności) 2) funkcja rosnąca dla x należących do R bez 0?

PW: Tak, ale stwierdzenie 2) jest silniejsze od 1), i należałoby użyć 2).

Jerzy: 17:13 Tak, f(−1) < f(1) sugeruje,że funkcja jest rosnąca.

Jerzy: 17:16 Funkcja jest rosnąca w całej dziedzinie.