wykaż Anka: W trójkącie prostokątnym ABC o przyprostokątnych 12 i 5 na przeciwprostokątnej BC wybrano punkt M tak,że obwody trójkątów ABM i ACM są równe. Wykaż,że stosunek promieni okręgów wpisanych w trójkąty ABM i ACM jest równy stosunkowi odcinków |BM|/|MC|

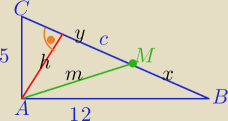
Mila: |BC|=c=13 5+y+m=12+x+m r_x− promien okręgu wpisanego w ABM r_y− promien okręgu wpisanego w ACM

PΔABM		x
	=		− Δ mają tę samą wysokość opuszczoną z wierzchołka A
PΔACM		y

odpowiednio na BM i CM Stąd:

12+x+m   *rx 2		x
	=		⇔
5+y+m   *ry 2		y

rx		|BM|
	=
ry		|CM|

cnw =======================

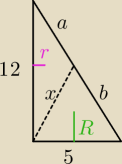
Blee: 5+b = 12+a −> b = 7 + a a + b = 13 −> 2a = 6 −> a = 3 −> b = 10

R		P1		5*b*sinα		5*b*(12/13)		b
	=		=		=		=
r		P2		12*a*sinβ		12*a*(5/13)		a

c.n.w.