Wykaż, że funkcja jest... D4n1s0: Cześć mam problem z zadaniem z funkcji. Nie wiem czy dobrze kombinuję i czy dobrze przekształciłem wzór. Zadanie: Wykaż, że funkcja: f(x) = 3x² +2 jest malejąca w przedziale (−∞,0) Zrobiłem to tak: Założenie: x₁ − x₂ <0, x₁ < 0 x₂ <0 więc x₁ + x₂ <0 Badam znak f(x₁) − f(x₂)

	3
3x12+2 − 3x22+2 = 3x12 − 3x22 + 4 = 3 [ (x1 − x2) (x1 + x2) +		]
	4

Iloczyn jest dodatni + liczba dodatnia czyli wyrażenie jest dodatnie. Pomnożone jeszcze przez 3 dalej daje liczbę dodatnią, więc f(x₁) − f(x₂) >0 Czy dobrze to zrobiłem? Analogicznie próbuję zrobić kolejny przykład, ale już coś mi nie wychodzi: Wykaż, że funkcja f(x) = −x² +3 jest rosnąca w przedziale (−∞, 0) Przekształcam: −x₁² +3 +x₂² +3 = −x₁² + x₂² +6 = −(x₁² − x₂² − 6) = − [(x₁ − x₂) (x₁ + x₂) −6] I co dalej? Iloczyn jest dodatni ale nie wiemy czy większy czy mniejszy od 6. Mógłby mi ktoś pomóc i wytłumaczyć?

Jerzy: Wystarczy pokamzać,że pochodna jest ujemna w tym przedziale.

Jerzy: W drugim zadaniu pokaż,że pochodna jest dodatnia w tym przedziale.

D4n1s0: Jestem w 1 klasie, nie brałem jeszcze pochodnych. Dopiero zacząłem dział z funkcji.

iteRacj@: badasz znak f(x₁) − f(x₂) ← tu jest dobrze −(x₁)² +3 +(x₂)² +3 ← tu masz błąd −(x₁)² +3 −[−(x₂)²+3]= ...

iteRacj@: 3x₁²+2 − 3x₂²+2 ← ten sam błąd

D4n1s0: A no tak, minus zmienia znak. Dzięki bardzo.

D4n1s0: Proszę jeszcze o sprawdzenie, nie wiem czy znowu coś robię źle: Zadanie: wykazać ze f(x) = x² − 2x jest malejąca, przedział (−∞,1) x₁² − 2x₁ − x₂² + 2x₂ = (x₁ − x₂)(x₁ + x₂) −2(x₁ − x₂) = ..... x₁ − x₂ <0, ale suma zgodnie z przedziałem to chyba x₁ + x₂ < 2 więc skąd mam wiedzieć czy jest dodatnia czy ujemna?

Milo: wyłączając przed nawias mamy = (x₁ − x₂)(x₁ + x₂ − 2) x₁ < x₂, więc pierwszy czynnik jest ujemny x₁ <1, x₂ < 1, więc x₁ + x₂ < 2 zatem drugi czynnik ujemny Czyli f(x₁) − f(x₂) > 0, gdzie x₁<x₂ f(x₁) > f(x₂) Na mniejszym argumencie większa wartość ⇒ funkcja jest malejąca

PW: (x₁ − x₂)(x₁ + x₂) −2(x₁ − x₂) = (x₁−x₂)(x₁+x₂−2) − przy założeniu x₁<x₂<1 oba czynniki są ujemne.

D4n1s0: Dzięki. Reszta już poszła, ale mam pytanie, jak udowodnić gdy mamy sumę przedziałów? Wykazać, że funkcja f(x) = −⁵_x nie jest rosnąca w zbiorze R₊ ∪ R₋ Po przekształceniu mam: f(x) = ^{5(x₁ − x₂)} _x1x2 x jest przecież i mniejszy i większy od 0. Mógłby ktoś wytłumaczyć?

Jerzy: Rozpatruj oddzielnie obydwa przedziały.

D4n1s0: W tym i w tym funkcja jest rosnąca.

Jerzy: Dokładnie tak.

Saizou :

	5
Załóżmy dla dowodu nie wprost, że funkcja f(x)=−		jest rosnąca w dziedzinie,
	x

tzn w zbiorze D=R\{0}=R₋ ∪ R₊. Skoro jest ona rosnąca, tzn. dla dowolnych x₁, x₂ ∊D takich, że x₁ < x₂ zachodzi f(x₁) < f(x₂). Weźmy x₁<0 oraz x₂>0 (wynika to z założenia dowolności x₁ oraz x₂), wówczas

	5		5
f(x1)=−		oraz f(x2)=−
	x1		x2

Zbadajmy różnicę

	5		5		−5x2+5x1		5(x1−x2)
f(x1)−f(x2)=−		−(−		=		=
	x1		x2		x1x2		x1x2

Iloczyn x₁•x₂ jest ujemny, bo x₁<0 i x₂>0 (czyli są przeciwnych znaków) różnica x₁−x₂ jest ujemna, bo x₁<x₂

	5(x1−x2)
zatem iloraz		=f(x1)−f(x2) jest dodatni
	x1x2

(jako iloraz dwóch liczb o tych samych znakach), co jest sprzeczne, bo f(x₁)−f(x₂)<0. Pokazaliśmy, że funkcja f nie jest rosnąca w swojej dziedzinie.

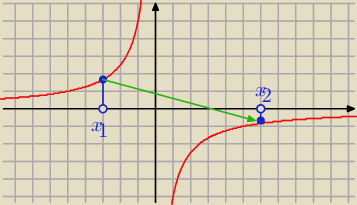
Saizou : Funkcja f jest przedziałami rosnąca, ale nie jest rosnąca w całej dziedzinie

Jerzy: Jest rosnąca w R₊ , jest rosnąca w R₋,ale nie jest rosnąca w całej dziedzinie.

Jerzy: