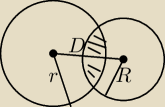
Oblicz pole zacieniowanej figury z dwóch kół o róznych promieniach. Dominik: Jak obliczyć pole zakreskowanej figury, jeżeli promienie kół są różne. r=4 R=3 D=4

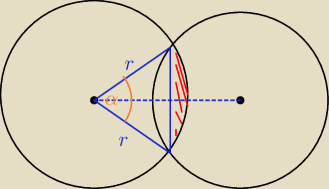
Blee: Wiesz jak obliczyć to czerwone pole ? To analogicznie później drugą część liczysz

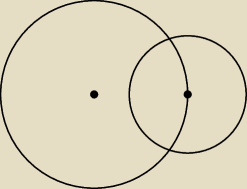
Blee: D = r Na pewno to wtedy masz taką sytuację

kupa 3 2 0: elo zwisie

kupa 3 2 0:

kupa 3 2 0: papryka

Dominik: @Blee Tylko jak obliczyć to czerwone pole jeżeli nie znam kąta alfa, bo z nim to obliczam wycinek koła, następnie pole tego trójkąta i odejmuje a co jeśli nie znam alfa?

Adamm: twierdzeniem Cosinusów R²=r²+D²−2rDcos(α/2) cos(α/2)=23/32 α=2arccos(23/32)

Mila: Dominik napisz dokładnie co oznaczasz literą D.

Dominik: D oznacza odległość od środka jednego okręgu do środka drugiego.

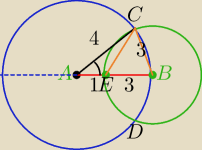
Mila: |AB|=4 P_ΔABC− z wzoru Herona

	4+4+3		11
p=		=		=5.5
	2		2

	3
PΔ=√5.5*(5.5−4)2*(5.5−3)=√5.5*(1.5)2*2.5=1.5*√5.5*2.5=		√55
	4

	1		3
PΔ=		*4*4 *sinα=		√55
	2		4

	3√55
sinα=		odczytujesz w tablicach
	32

α≈44^o

Dominik: @Mila dzięki wielkie

Mila: Skąd masz to zadanie?

a&b: 2 sposób

	3		√55
ΔABC równoramienny to h=√16−(		)2=
	2		2

	3
P=		√55 i P=8sinα
	4

	3√55
to sinα=
	32

α≈44^o

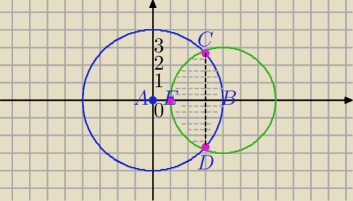
Mila: x²+y²=16 i (x−4)²+y²=9 Punkty przecięcia :

	23		3√55
C=(		,		)
	8		8

	23		3√55
D=(		,		)
	8		8

P=2*₀∫^(3√55)/8(4+√9−y²−√16−y²) dy≈2*7.879

Dominik: Zadanie jest z platformy do nauki programowania

Mila: