proszę o rozwiązanie Anna: rozwiąż równanie f(x) = { IxI − 3 ; IxI >2

	1
{ −(		)3 ; IxI ≤ 2
	2

określ liczbę rozwiązań równania

	1		1		1		1
f(x) =		log		m4 tu ma być		log przy podstawie		z m4
	4		4		4		4

narysuj wykres h(m) określająca tę liczbę rozwiązań

Jerzy: A o jakie równanie chodzi ?

Anna: w takiej formie było podane ja myślę że tu są zawarte dwa zadania jedno to f(x) a drugie to z logarytmem

Jerzy: Na pewno dwa,tylko w obu przypadkach nie wiadomo , o co chodzi.

Anna: bardzo mi przykro ale tak było napisane jeżeli dowiem się jak naprawdę jest poprawnie zapisane to ponownie poproszę o radę dziękuję

inf: Jeśli chodzi o zad. 2 (z logarytmami) podejrzewam, że funkcja ma postać

	1
f(x)=		log14m4. Zatem korzystając z własności logarytmu − potęgę przenosisz
	4

	1
przed logarytm − wtedy 4 skraca Ci się z		i zostaje log14m − a to jesteś w
	4

stanie bez problemu rozwiązać korzystając z dziedziny logarytmu

inf: Zad. 1 to przede wszystkim nie równania, a układ równań Zamieniasz wartość bezwzględną na przedziały i w wyznaczonych przedziałach analizujesz liczbę rozwiązań każdego z równań układu, pamietając, że między warunkiem a rozwiaząniem układu jest spójnik "i".

inf: Możesz też narysować analizowany wykres funkcji (przedziałami) oraz zaznaczyć warunki co do "x" i określić liczbę punktów wspólnych

Jerzy: Klub jasnowidzów ?

iteRacj@: Po przeczytaniu tego zadania miałam przekonanie, zadanie jest niezrozumiałe i tak jak Jerzy wrażenie, że coś jest źle przepisane. Teraz widzę, że to jest zadanie jedno zadanie i jest w nim równanie, bo jest podobne do 484 ze zbioru p.Kiełbasy. Za godzinę wpiszę rozwiązanie, chyba że ktoś rozwiąże wcześniej.

Pytający: Inf, poprawka:

1
	log1/4(m4)=log1/4|m|, m≠0.
4

	1
Natomiast f(x)=		log1/4(m4) jest funkcją stałą (przecież x jest zmienną, a wartość
	4

zależy od m). Jak zauważył Jerzy, treść są "nieco" zagadkowe.

Jerzy: Moim zdaniem w obydwu przypadkach jest pytanie o własność funkcji

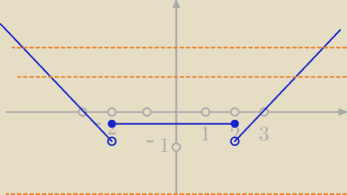
iteRacj@: mój wkład do klubu interpretatorów (jasnowidzów?) Dana jest funkcja określona wzorem f(x)={IxI−3; dla IxI>2 {−(1/2)³; dla IxI ≤ 2 zapiszemy tę funkcję tak, żeby narysować łatwo jej wykres f(x)={IxI−3; dla x<−2 i dla x>2

	1
{−		; dla −2≤x≤ 2
	8

	1
a/ określ liczbę rozwiązań równania f(x)=		*log1/4(m4), zał. m≠0
	4

po lewej stronie równania jest wyjściowa funkcja opisana wzorem powyżej, po prawej funkcja

	1
stała y=0*x+b, gdzie wartość b=		*log1/4m4 zależy w opisany sposób od parametru m
	4

stąd mamy

	1
brak rozwiązań dla (		*log1/4(m4) )∊(−∞,−1>
	4

	1		1		1
dwa rozwiązania dla (		*log1/4(m4) )∊(−1;−		)U(−		;∞)
	4		8		8

	1		1
nieskończenie wiele dla (		*log1/4(m4))∊{−		}
	4		8

na podstawie tego trzeba określić ilość rozwiązań w zależności od m b/ narysuj wykres h(m) określająca tę liczbę rozwiązań to druga część polecenia

Anna: przepraszam jeszcze raz

	1		1
wkradł się błąd w funkcji f(x) ma być −(		x)3 a nie −(		)3
	2		2

ite: w takim razie zacznij od narysowania wykresu funkcji f(x)={IxI−3; dla IxI>2

	−x3
{		; dla IxI ≤ 2
	8