pochodna mat: Wyznacz na paraboli y=−x²+9 taki punkt o dodatnich współrzędnych, aby styczna do paraboli poprowadzona w tym punkcie ograniczała wraz z osiami układu współrzędnych trójkąt o najmniejszym polu. Wiem, że było już tu takie zadanie, jednak nie rozwiało moich wątpliwości, dlatego pytam. Otóż. Wyznaczam pochodną f'(x)=−2x. Przyjmuje punkt jako P=(x₀,−x_o²+9). Tu we wszystkich rozwiązaniach pojawia się taki wzór: y−y(xo)=y′(xo)(x−xo). No okej. Można. Ale chcę iść inną drogą. Podstawiam współrzędne punktu P do równania prostej: y=ax+b. Wyznaczam stąd b=−x₀²+9+2xx₀. Podstawiam następnie to do równania y=ax+b, zatem y=−2x*x₀+−x₀²+9+2xx₀. I w tym momencie zeruje mi się wyrażenie z x₀x. Poprawny wzór stycznej w tym miejscu powinien wyjść: y=−2xx₀+x₀²+0. Mógłby ktoś mi wyjaśnić, w którym miejscu popełniam błąd i ewentualnie nakierować na prawidłowe rozwiązanie? Dalsze kroki rozwiązania potrafię wykonać, więc nie potrzebuje całego obliczenia. Proszę tylko o ten jeden krok.

PW: Podstawiasz współrzędne punktu P do równania prostej: y₀=−2x₀+b, czyli −x₀²+9=−2x₀+b b=−x₀²+2x₀+9. Krótko mówiąc − jeżeli podstawiasz coś w miejsce "x", to już tego "x" nie będzie, tylko konkretna liczba. A u Ciebie zostało 2x^.x_o.

mat: Racja. Dziwne to. W każdym razie dzięki.

mat: Chociaż... Czy to jest na pewno dobre rozwiązanie? Podstawiam to do wzoru y=ax+b. a=−2x, b=−x₀²+2x₀+9. Z tego nie wyjdzie y=−2xx₀+x₀²+9 − a tak powinno wyjść.

Blee: Czemu a = −2x Skad ten − i skad ten x

mat: Bo a=f'(x), no nie?

mat: A x to pierwsza współrzędna punktu P

mat: No bo niby do czego mam to podstawić? Podstawiając do y₀=−2x₀+b wyjdzie mi masło maślane, bo dostanę wzór, który był podany w treści zadania Z tego względu podstawiam to do y=ax+b Mam wyliczone b=−x₀²+2x₀+9 Dlaczego współczynnik kierunkowy a nie jest równy w tym przypadku pochodnej funkcji?

mat: ?

Pytający: (x₀,−x₀²+9) y=ax+b // a=−2x₀ y=−2xx₀+b b=y+2xx₀=(−x₀²+9)+2(x₀)x₀=x₀²+9 y=−2xx₀+x₀²+9

PW: Równanie stycznej ma postać (1) y=ax+b, w równaniu tym a=f'(x₀), gdzie x₀ oznacza pierwszą współrzędną punktu styczności. U nas zatem a=−2x₀ (f'(x)=−2x, a więc dla x=x₀ mamy f'(x₀)=−2x₀ − tu był błąd w rozumowaniu). Zgodnie z (1) równanie stycznej ma postać (2) y=(−2x₀)x+b. Jeżeli prosta (2) ma być styczną w punkcie (x₀, f(x₀)), to podstawiamy x=x₀ i y=f(x₀)=−x₀²+9: f(x₀)=−2x₀x₀+b, czyli −x₀²+9=−2x₀²+b, b=x₀²+9. Styczna (2) ma więc równanie y=(−2x₀)x+x₀²+9

mat: Teraz się zgodzę. Dziękuję serdecznie!

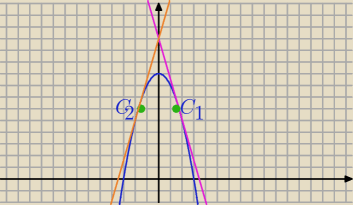
Mila: 1) f(x)=−x²+9 C=(c, −c²+9) punkt styczności 2) y=f'(c)*(x−c)+f(c) − równanie stycznej f'(x)=−2x f'(c)=−2c Styczna : s: y=(−2c)*(x−c)+(−c²+9)⇔ s: y=−2cx+c²+9 3) Pole Δ: Miejsce zerowe: −punkt przecięcia OX przez styczną: −2c*x+c²+9=0

	c2+9
x0=
	2c

Punkt przecięcia OY przez styczną: −2c*0+c²+9=y₀ y₀=c²+9

	1		c2+9
PΔ(c)=		*(c2+9)*
	2		2|c|

c>0

	3*(c2−3)*(c2+9)
P'(c)=
	4c2

P'(c)=0⇔c=√3 i C=(√3,6) styczna : s: y=−2√3x+12 ==================] Dodatkowo drugi przypadek: Lub c<0 c=−√3 i C=(−√3, 6) s: y=2√3+12 ============ Sprawdzaj rachunki.

Mila: O, niepotrzebnie pisałam, bo PW był szybszy