czworokąt
Manfred: ABCD jest czworokatem wypukłum w którym ∡CAB=∡CAD,∡BCA=∡ACD.
Pokaż że ∡BCM=∡DBA gdzie M jest srodkiem boku AB.
7 lip 17:02
iteRacj@:
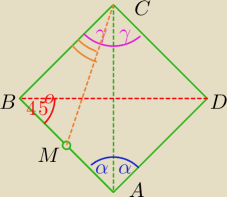
ABCD jest dowolnym czworokątem wypukłym np. kwadratem
|∡CAB|=|∡CAD|=
α=45
o |∡BCA|=|∡ACD|=
γ=45
o
|∡DBA|=45
o
|AM|=|BM|≠0 → ∡ACM>0
o
|∡BCM|=|∡BCA|−|∡ACM|=45
o−|∡ACM|<45
o
|∡BCM|≠|∡DBA|
7 lip 17:53
Manfred: Ale to nie musi byc kwdarat?
7 lip 17:55
7 lip 17:58
Manfred: co?
7 lip 18:01
iteRacj@:
Nie można wykazać, że w dowolnym (czyli w każdym) czworokącie wypukłym spełnione jest
równanie z tezy, skoro istnieje taki czworokąt wypukły (kwadrat), dla którego taka równość nie
zachodzi.
Teraz można się tylko zastanawiać, czy istnieje jakikolwiek czworokąt wypukły, dla którego teza
jest prawdziwa.
7 lip 18:05
 ABCD jest dowolnym czworokątem wypukłym np. kwadratem
|∡CAB|=|∡CAD|=α=45o |∡BCA|=|∡ACD|=γ=45o
|∡DBA|=45o
|AM|=|BM|≠0 → ∡ACM>0o
|∡BCM|=|∡BCA|−|∡ACM|=45o−|∡ACM|<45o
|∡BCM|≠|∡DBA|
ABCD jest dowolnym czworokątem wypukłym np. kwadratem
|∡CAB|=|∡CAD|=α=45o |∡BCA|=|∡ACD|=γ=45o
|∡DBA|=45o
|AM|=|BM|≠0 → ∡ACM>0o
|∡BCM|=|∡BCA|−|∡ACM|=45o−|∡ACM|<45o
|∡BCM|≠|∡DBA|