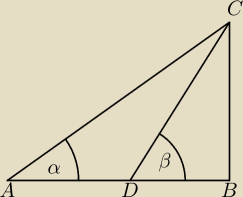
trójkąt do podstawień usuwających niewymierność z trójmianem kwadratowym Mariusz: W trójkącie ABC długości dwóch boków są dane

	x		x		x
Oznaczmy je tak aby sinα =		lub tgα =		lub secα =
	a		a		a

Niech CD będzie dwusieczną kąta C , wprowadźmy nową zmienną

	CB
tak aby u =
	BC

Wyraź długości boków trójkąta ABC za pomocą wprowadzonej zmiennej Jeśli chodzi o rysunek to być może przydało by się coś jeszcze dorysować aby lepiej było widać jak należy wyrazić długości boków trójkąta ABC za pomocą wprowadzonej zmiennej Na pomysł takiego zadania wpadłem po tym jak zobaczyłem u amerykańców trójkąt dla podstawienia cyklometrycznego U Gewerta i Skoczylasa znalazłem trójkąt dla tzw podstawienia uniwersalnego którego amerykańcy nazywają podstawieniem Weierstrassa i chciałem narysować coś podobnego dla podstawień zbliżonych do podstawień Eulera

	CB
(Podstawienia Eulera wyprowadza się nieco inaczej ale podstawienie u =
	BD

będzie bardzo podobnie wyglądać i także usunie niewymierność z całki)

Blee:

	CB
Zacznijmy od tego: u =
	BC

Mariusz:

	CB
Powinno być u =
	BD

czyli u = tgβ Napisałem to w ostatnim zdaniu tego wpisu a to co ty zacytowałeś to wygląda na literówkę