zadaniematuralne
zadaniematuralne: Punkt A = (7,− 1) jest wierzchołkiem trójkąta równoramiennego ABC , w którym |AC| = |BC| .
Obie współrzędne wierzchołka C są liczbami ujemnymi. Okrąg wpisany w trójkąt ABC ma równanie
x2 + y2 = 10 . Oblicz współrzędne wierzchołków B i C tego trójkąta.
Wiem, że jest to zadanie maturalne i w internecie jest pełno rozwiązań, jednak nie mogę
zrozumieć pierwszego kroku każdego z tych rozwiązań. Zacytuje z CKE:
"Proste AC i AB przechodzą przez punkt A = (7, −1), żadna z nich nie jest prostopadła do osi Ox
układu współrzędnych, więc mają równania postaci
y = a(x−7)−1"
Mógłby mi ktoś wytłumaczyć skąd wzięło się to równanie?
1 lip 19:30
Sushi:
czy zrobiłaś/eś rysunek do zadania ?
1 lip 19:34
zadaniematuralne: Tak.
1 lip 19:36
Sushi:
i co z niego wynika ?
1 lip 19:36
Sushi:
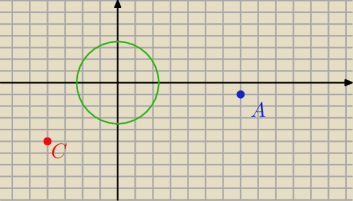
1 lip 19:38
zadaniematuralne: W zasadzie nic. Mam płaszczyznę kartezjańską, na której jest zaznaczony punkt A=(7,−1). Wiem,
że C ma obie współrzędne ujemne, zatem leży w III ćwiartce. Wiem, że okrąg o środku S=(0,0) i
promieniu √5 jest wpisany w trójkąt, zatem jest styczny do poszczególnych prostych. Kolejne
etapy rozumiem. Nie potrafię zrozumieć tylko tego pierwszego − skąd wzięło się to równanie
a(x−7)−1...
1 lip 19:40
zadaniematuralne: *y=a(x−7)−1
1 lip 19:41
Sushi:
wzór na prostą przechodzącą przez punkt
y−yA=a(x−xA)
1 lip 19:41
zadaniematuralne: W sumie racja. Dziękuję!
1 lip 19:42
Sushi:
na zdrowie

1 lip 19:43

