Geometria Kaj: Znaleźć równanie ogolne prostej ich wspólnej płaszczyzny L1:{ x=1+t y=−1+2t Z=t L2:. { x=2−2t y=−1−4t z=1−2t Proszę o pomoc w tym zadaniu

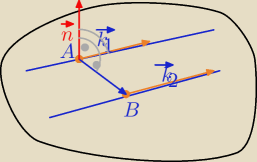
Mila: k₁^→=[1,2,1] − wektor kierunkowy prostej L₁ k₂^→=[−2,−4,−2]− wektor kierunkowy prostej L₂ Proste są równoległe. A=(1,−1,0)∊L₁ B=(2,−1,1)∊L₂ AB^→=[1,0,1] n^→=[1,2,1] x [1,0,1] =[2,0,−2] −wektor normalny szukanej płaszczyzny π: 2*(x−1)−2*z=0 2x−2z−2=0 π: x−z−1=0 ==========

Kaj: Dziękuję bardzo

Mila: I czego tu nie rozumiesz?

Mila: 1) [1,2,1] || [−2,−4,−2] ponieważ:

1		2		1
	=		=
−2		−4		−2

Zatem proste są równoległe , ponieważ wektory kierunkowe tych prostych są równoległe. 3) równanie płaszczyzny : Patrz rysunek n^→=k₁^→ x AB^→=[2,0,−2] A=(1,−1,0) 2*(x−1)−0*(y+1)−2*(z−0)=0 2x−2z−2=0 /:2 x−z−1=0 =========

Mila: 4) Odległość prostych:

	|k1 x AB|		√22+02+(−2)2		√8
d=		=		=
	|k1|		√1+22+1		√6

	2√3
d=
	3