Uklad 6.167: bliczyć odległość punktu A(0 0 0) od płaszczyzny przechodzącej przez punkty B(1 0 0) C(0 2 0) D(0 0 3) Przepraszam że ponawiam pytanie ale chciałabym prosić o pomoc z znalezieniem wzoru płaszczyzny nie umiem przeksztalcic tych punktów

jc: Skąd bierzesz takie egzotyczne oznaczenia A(0,0,0)? Prawie jak w programie w javie.

6.167: Zadanie takie

jc: Chodzi o oznaczenie A(0,0,0). Zupełny brak spójności z innymi oznaczeniami. Takie oznaczenia sprawiły, że przez lata nie strasznie nie lubiłem geometrii analitycznej. f(3) oznacza, że f ma wartość 3, No właśnie, czy można tak napisać? Czy raczej tak f(3) ma wartość 3, a jak napisać, że funkcja f w punkcie 7 przyjmuje wartość 3? f(7)(3), f(7,3) czy jeszcze jakoś inaczej? A jak dodać dwie zmienne? Same kłopoty i potem już nie można patrzyć na zadanie.

6.167: Ehh sam zaczynam się zniechęcać do tego zadania jak i działu...

Mila: B=(1 ,0, 0) ,C=(0, 2, 0), D(0 ,0 ,3) π: Ax+By+Cz+D=0 podstawiasz wsp. punktów A+D=0 2B+D=0 3Z+D=0 A=−D

	1
B=−		D
	2

	1
Z=−		D
	3

	1		1
π: −D*x−		Dy−		Dz+D=0 ⇔
	2		3

	1		1
−x−		y−		z+1=0 *(−6)
	2		3

π: 6x+3y+2z−6=0 ====================== II sposób BC^→=[−1,2,0] BD^→=[−1,0,3] n^→=[−1,2,0] x[−1,0,3]− wektor normalny płaszczyzny i j k −1 2 0 −1 0 3 Liczysz wyznacznik W=6i+3j+2k n^→=[6,3,2] Równanie płaszczyzny: B=(1 ,0 ,0)∊π π: 6*(x−1)+3*(y−0)+2*(z−0)=0 π: 6x+3y+2z−6=0 ================

	|6*0+3*0+2*0−6|		6		6
d(A,π)=		=		=
	√62+32+22		√49		7

jc: Już lepiej byłoby pisać (A,0,0,0). Wtedy punkt składałby się z nazwy i 3 współrzędnych. Ale może chodzi o to, że punkt jest jakimś abstrakcyjnym obiektem, dla którego możemy określić współrzędne. Wtedy napisałbym to raczej tak: A→(0,0,0) lub w jakiś sposób nazwał funkcję, która przypisuje punktowi współrzędne np. f. Wtedy mielibyśmy f(A)=(0,0,0). Wydaje się, jednak, że najprościej rozważać R³ i pisać A=(0,0,0). Punkty (a,0,0), (0,b,0), (0,0,c) o ile a,b,c ≠0, wyznaczają płaszczyznę x/a + y/b + z/3 =1. Czy to nie jest oczywiste? Dalej możemy skorzystać ze wzoru na odległość punktu (x₀, y₀, z₀) od płaszczyzny Ax+By+Cz+D=0.

	|Ax0+By0 + Cz0 + D|
odległość =
	√A2+B2+C2

jc: Tam miało być x/a+y/b+z/c=1. Niektórzy mówią, że to równanie odcinkowe płaszczyzny.

Mila: Najprościej w tym przypadku napisać równanie odcinkowe tej płaszczyzny, ale mało kto o tym równaniu pamięta. Pozdrawiam.

Mila: Równanie płaszczyzny w R3. https://pl.wikipedia.org/wiki/P%C5%82aszczyzna

6.167: Dziękuję chyba rozumiem 2 sposób... A to już wiele dziękuję jeszcze raz

jc: Mila, jak ja mamy iloczyn wektorowy [6,3,2], to możemy policzyć

	1
pole trójkąta BCD. Pole =		(√62+32+22}=7/2.
	2

Objętość czworościanu ABCD = 1*2*3/6=1. h * (7/2) /3 = 1. Stąd h=6/7.

jc: Przy okazji, na pewno bez liczenia odpowiesz, ile wynosi pole czworościanu ABCD.

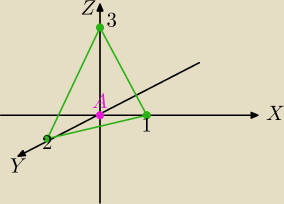
Mila: Rysunek dla autorki wpisu.

6.167: Tylko nwm dlaczego wzór wychodzi mi 6x+2y+3z−6

6.167: Autora

6.167: Słownik poprawił na autorkę w pierwszym wpisie...

pawel32: wyznacznik mam (6 2 3)

Mila: i j k || i j −1 2 0 || −1 2 −1 0 3 || −1 0 W=i*2*3+j*0*(−1)+k*(−1)*0−(j*(−1)*3−i*0−k*2*(−1)) W=6i −(−3j+2k) W=6i+3j+2k n^→=[6,3,2] − wektor normalny płaszczyzny

Mila: W tym zadaniu najlepiej napisać równanie odcinkowe płaszczyzny, ponieważ masz dane 3 punkty płaszczyzny jak na rysunku.

	x		y		z
π:		+		+		=1 /*6
	1		2		3

stąd inna postać równania: π: 6x+3y+2z−6=0 i liczysz odległość A =(0,0,0) od tej płaszczyzny