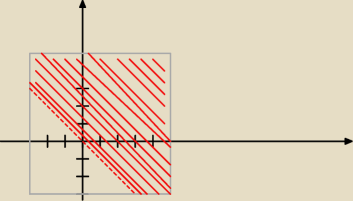
 Losuje dwie liczby z odcinka [−3,5]. Jakie jest prawdopodobieństwo, że ich suma jest dodatnia,
jeżeli jedna z nich jest dodatnia?
|Ω| = [−3,5] x [−3,5] = 64
x+y >0 gdy x>0 lub,
x+y >0 gdy y>0
Losuje dwie liczby z odcinka [−3,5]. Jakie jest prawdopodobieństwo, że ich suma jest dodatnia,
jeżeli jedna z nich jest dodatnia?
|Ω| = [−3,5] x [−3,5] = 64
x+y >0 gdy x>0 lub,
x+y >0 gdy y>0
| 1 | ||
A = 64 − ( | * 6 * 6) = 64 − 18 = 46 | |
| 2 |
| 46 | ||
P(A) = | ||
| 64 |
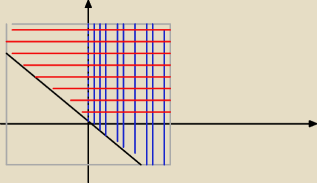 I jeszcze mam taki pomysł jak na rysunku powyżej.
Która opcja poprawna?
Bo gdyby w poleceniu było tylko, że suma ma być dodatnia, to opcje pierwsza była by dobra.
W przypadku gdy mam, że jeśli jedna z nich jest dodatnia, to zastanawiam się nad drugą.
Czy tutaj to trzeba w ogóle inaczej liczyć?
Pozdrawiam
I jeszcze mam taki pomysł jak na rysunku powyżej.
Która opcja poprawna?
Bo gdyby w poleceniu było tylko, że suma ma być dodatnia, to opcje pierwsza była by dobra.
W przypadku gdy mam, że jeśli jedna z nich jest dodatnia, to zastanawiam się nad drugą.
Czy tutaj to trzeba w ogóle inaczej liczyć?
Pozdrawiam
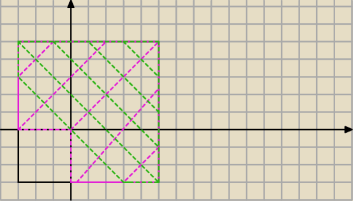
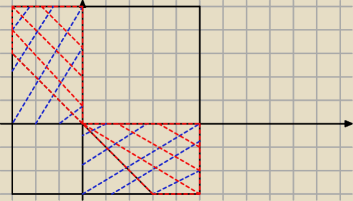 Jakie jest prawdopodobieństwo, że ich suma jest dodatnia, jeżeli jedna z nich jest dodatnia?
To będzie prawdopodobieństwo warunkowe.
A // suma jest dodatnia
B // dokładnie jedna z nich jest dodatnia
C // przynajmniej jedna z nich jest dodatnia
Jakie jest prawdopodobieństwo, że ich suma jest dodatnia, jeżeli jedna z nich jest dodatnia?
To będzie prawdopodobieństwo warunkowe.
A // suma jest dodatnia
B // dokładnie jedna z nich jest dodatnia
C // przynajmniej jedna z nich jest dodatnia
| P(A∩B) | |A∩B| | (64−18)−5*5 | 21 | |||||
P(A|B)= | = | = | = | =0.7 | ||||
| P(B) | |B| | 2*3*5 | 30 |
| P(A∩C) | |A∩C| | 64−18 | 46 | |||||
P(A|C)= | = | = | = | |||||
| P(C) | |C| | 64−3*3 | 55 |
