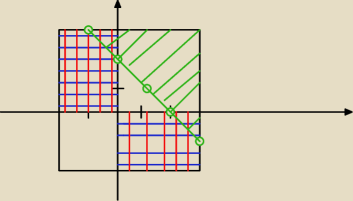
prawdopodobienstwo geometryczne Bartek: Z odcinka [−2,3] losujemy dwie liczby, mamy zdarzenia: A − iloczyn wylosowanych liczb jest ujemny B − Suma wylosowanych liczb jest mniejsza od 2 Obliczyć P(A), P(B), P(B|A), czy zdarzenia A i B są nie zależne? |Ω| = [−2,3] x [−2,3] = 25 A − x*y < 0, więc: x<0 i y>0, oraz: x>0 i y<0 (kolory niebieski i czerwony) A = 2*3 + 3*2 = 12

	12
P(A) =
	25

B − x+y<2 y=−x+2

	1
B =		* 4 * 4 = 8
	2

	8
P(B) =
	25

	P(BnA)
P(B|A) =
	P(A)

(BnA) to będą te dwa trójkąciki?

	1
(BnA) = 2 * (		* 1 * 1) = 1
	2

	1
P(BnA) =
	25

	1		12		1
P(B|A) =		/		=
	25		25		12

Czy są niezależne? P(AnB) = P(A) * P(B)

1		12		8
	=		*
25		25		25

Sprzeczność, więc zą zależne. Proszę o sprawdzenie, dziękuje

zielony: zielony obszar który zaznaczyłeś spełnia warunek x+y>2

Blee: B na pewno jest zle policzone

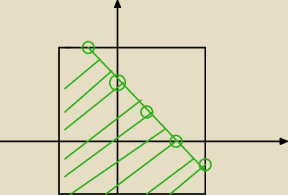Bartek: ahh, co za głupi błąd.. W takim razie A= 25 − 8 = 17

	17
P(B) =
	25

	P(BnA)
P(B|A) =
	P(A)

BnA = 4

	4
P(BnA) =
	25

	4		12		1
P(B|A) =		/		=
	25		25		3

Czy nadal gdzię sie myle? Dziękuje

Bartek: a nie, pomyliłem się w warunkowym, zaraz poprawie.

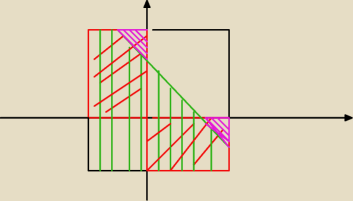Bartek: BnA = 11 bo to są te pola ze zdarzenia A, odjąć dwa trójkąciki (fioletowe), bo nie są częścią wspólne

	11
P(BnA) =
	25

	11		12		11
P(B|A) =		/		=
	25		25		12

P(A)*P(B) ! = (AnB)

12		17		11
	*		!=
25		25		25

Czy teraz jest dobrze?

Bartek: odświeżam

Pytający: Tak.