Dowód geometryczny
Karolina: Mogłabym prosić o jakąś wskazówkę? Zad. Dany jest trójkąt ostrokątny równoramienny ABC, w
którym AC=BC. W tym trójkącie poprowadzono wysokość AD. Udowodnij, że kąt ABC jest dwa razy
większy od kąta BAD.
Ułożyłam działania
2α+β=180
α−δ+β=90
β=2α
Ale jak udowodnić to o co pytają? Z góry dziękuję
22 cze 22:52
Mila:
To jest niemożliwe, masz błąd w treści.
22 cze 23:03
iteRacj@:
a równobocznym (oczywiście szczególny przypadek) tak nie jest?
22 cze 23:14
Karolina: Przepisałam identycznie zadanie z podstawy programowej men dla VII−VIII kl. . Ja też uważam, że
jest błąd. Dziękuję.
22 cze 23:14
Karolina: Ale pewna na 100% nie jestem
22 cze 23:15
Mila:
Tak
Iteracjo, tylko w równobocznym.

Treść jest taka:
(ostatnie zdanie)
Udowodnij, że kąt ACB jest dwa razy większy od kąta BAD.
Teraz
Karolino poradzisz sobie?
22 cze 23:37
Karolina: Tak,
α+2(90−γ)=180
α=2γ
Czyli tamta treść była zła?
22 cze 23:43
Mila:
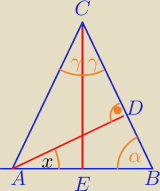
|AC|=|BC|
∡A=∡B=α
1) Wysokość CE jest dwusieczną kąta C
∡x=∡γ
∡ACB=2*x
23 cze 00:07
 Treść jest taka:
(ostatnie zdanie)
Udowodnij, że kąt ACB jest dwa razy większy od kąta BAD.
Teraz Karolino poradzisz sobie?
Treść jest taka:
(ostatnie zdanie)
Udowodnij, że kąt ACB jest dwa razy większy od kąta BAD.
Teraz Karolino poradzisz sobie?
 |AC|=|BC|
∡A=∡B=α
1) Wysokość CE jest dwusieczną kąta C
∡x=∡γ
∡ACB=2*x
|AC|=|BC|
∡A=∡B=α
1) Wysokość CE jest dwusieczną kąta C
∡x=∡γ
∡ACB=2*x