Kombinatoryka pomocy xxx: Witam pomoże ktoś z 6 zadaniami z kombinatoryki? Bardzo prosilbym o wytlumaczenie. 1. Znajdź funkcję tworzącą do ciągu danego zaleznoscia rekurencyjna : 2a_n+3=a_n+2a_n+1−a_n+2 2. Wykaż powyższą tożsamość kombinatoryczna:

	k i
[n+m]k=∑i=o		[n]i*[m]k−i

3. a)Rzucamy 5−ma kostkami i na każdej z tych kostek na jej scianach (po jednej) litery ze zbioru [A,B,C,D,E,F]. Z wszystkich literek układamy wyrazy .Ile takich roznych wyrazow mozna uzyskać? b) Ile roznych kolorowych wyrazow mozna uzyskac , jesli dodatkowo− kazda z kostek jest pomalowana jednym z pieciu kolorow: zielony, czerwony , blekitny, fiolotowy, zolty? 4. Rozmieszczamy przy okraglym stole n par malzenskich tak by zadna para nie siedziala obok siebie .Ile jest takich rozmieszczen?(wyprowadz wzor ogolny) 5. Ile jest k−elementowych podzbiorow zbioru liniowo uporzadkowanego n−elementowego (X,≥) takich w ktorych nie ma pary elementow bezposrednio sasiadujacych ze soba wzgledem porzadku ≥. 6. W rodzinie Ω zbiorow z powtorzeniami o elementach z danego (skonczonego) zbioru X relacje "zawierania" definiujemy w naturalny sposob gdy f,g ∊Ω to f ⊂ g oznacza, ze kazdy element z X wystepujacy w f, wystepuje tez w g nie rzadziej niz w f . Czy liczba takich k −elementowych "podzbiorow" ustalonego zbioru f ∊Ω zalezy tylko do mocy f? (Jesli tak to udowodnij, jesli nie podaj kontrprzyklad)

xxx: pomoze ktos? w zadaniu 3 mi wyszlo A) 6⁵ B) 5!*6⁵

xxx: wazne, jutro musze to przedstawic

xxx: @Mila pomozesz?

xxx: bardzo prosze o pomoc udalo mi sie zrobic zadanie 2. zostalo 1,4,5,6

xxx: 1) czy w zadaniu 1 najpierw powinienem obliczyc wzor ogolny z rownania charakterystycznego, a nastepnie przedstawic w postaci funkcji tworzacej?

Adamm: obojętnie ja bym liczył najpierw równaniem charakterystycznym

Mila: 1)

	1		1
an+3=		an+an+1−		an+2
	2		2

	1		1
an=		an−3+an−2−		an−1
	2		2

A(x)=∑(n=0 do ∞)a_nxⁿ=a₀+a₁*x+a₂*x²+∑(n=3 do ∞)a_nxⁿ=a₀+a₁*x+a₂*x²+

	1		1
+		∑(n=3 do ∞)an−3 xn+∑(n=3 do ∞)an−2xn−		∑(n=3 do∞an−1xn⇔
	2		2

A(x)=a₀+a₁*x+a₂*x²+

	1
+		x3∑(n=3 do ∞)an−3 xn−3+x2∑(n=3 do ∞)an−2xn−2−
	2

1
	*x∑(n=3 do∞)an−1xn−1=
2

	1
=a0+a1*x+a2*x2+		x3*∑(n=0 do ∞)anxn+x2*(∑(n=0 do∞)anxn−a0)−
	2

	1
+		*x*(∑(n=0 do∞)an−1xn−1−a0−a1*x)⇔
	2

	1		1
A(x)=a0+a1*x+a2*x2+		x3*A(x)+x2*(A(x)−a0)−		x*(A(x)−a0−a1x)
	2		2

	1		1		1
A(x)*(1+		x−x2−		x3)=(a2−a0)*x2+		(3a1+a0)*x+a0
	2		2		2

	1   (a2−a0)*x2+ (3a1+a0)*x+a0   2
A(x)=
	1   1   (1+ x−x2− x3)   2   2

======================================= Posprawdzaj rachunki. Może Mariusz tu spojrzy, lubi funkcje tworzące

xxx: zapomnialem napisac ze a0=a1=a2=1

xxx: zostalo zadanie 4 5 i 6 ktos sie podoła ?

xxx: zlitujcie się, bardzo ważne a kompletnie nie wiem jak zrobić...

Pytający: 4. a₀=1 a₁=0 a₂=2 a_n=(2(n−1))(2(n−1)−1)a_n−1 dla n≥3 // żonę dosadzamy na jedno z 2(n−1) miejsc, męża na jedno z (2(n−1)−1) miejsc Skąd: a₀=1 a₁=0 a_n=(2(n−1))! dla n≥2 // co "widać", a jeśli nie widać, to można np. indukcyjnie udowodnić 6. Nie zależy tylko do mocy f, kontrprzykład: X={1,2} • f={1,1,2}∊Ω, |f|=3 {1,1}⊂f, {1,2}⊂f // znaczy mamy 2 "podzbiory" 2−elementowe • f={1,1,1}∊Ω, |f|=3 {1,1}⊂f // znaczy mamy 1 "podzbiór" 2−elementowy

xxx: Dziękuje serdecznie Pytający. Mógłbyś bardziej rozwinąć sens zadania 4 bo w ogóle go nie widzę. W zadaniu 6 jest od mocy f. to nie zmienia wyniku zadania?

Pytający: No przecież w 6 zaznaczyłem, że w obu przypadkach |f|=3, a liczby podzbiorów 2−elementowych są różne. Dla |f|=2 też można podać: • f={1,2}∊Ω, |f|=2 {1}⊂f, {2}⊂f // znaczy mamy 2 "podzbiory" 1−elementowe • f={1,1}∊Ω, |f|=2 {1}⊂f // znaczy mamy 1 "podzbiór" 1−elementowy Co do 4: a₀, a₁, a₂ są oczywiste, możesz narysować odpowiednie ustawienia. 2 możliwe ustawienia dla n=2: A₁B₁A₂B₂ lub A₁B₂A₂B₁ jak można "dosadzić" do tych 2 par (rozsadzonych już zgodnie z zasadami) trzecią (n=3) parę? Ano masz (2*(3−1)) możliwych miejsc (powiedzmy z prawej (bo mowa o okrągłym stole) każdej z 2(n−1) już siedzących osób): A₁☐B₁☐A₂☐B₂☐ Zatem tę trzecią parę możesz dosadzić na (2(n−1))(2(n−1)−1) sposobów (tu: 2(3−1)(2(3−1)−1)=4*3). I taki tu sens.

Mila: Napisałeś warunki początkowe, to będę mogła sprawdzić funkcję tworzącą, czy nie ma błędu, ale dopiero po 20

jc: a₃ = 4!=24 ? A nie 192 ? ABCABC ABCBAC ABCACB ABACAB Możemy permutować A,B,C i w każdym małżeństwie zamieniać męża z żoną. Zobacz tutaj: http://mathworld.wolfram.com/MarriedCouplesProblem.html

xxx: Pytajacy juz rozumiem!. super wyjasniles. zostało tylko zadanie 5 .czy w zadaniu 5 podzielic ten zbior na liczby parzyste i nie parzyste?

xxx: w sumie tego nie uwzglednilismy w zadaniu 4. a mozna to jakos zrobic uzywajac zasady wlaczen i wylaczen?

Pytający: 5. Tu można narysować coś w stylu trójkąta Pascala (wyjdzie nieco zmodyfikowany). Oznaczmy: a(n,k) // szukana liczba k−elementowych podzbiorow zbioru liniowo uporzadkowanego n−elementowego (X,≥) takich w ktorych nie ma pary elementow bezposrednio sasiadujacych ze soba wzgledem porzadku ≥ Znowuż dość oczywiste warunki początkowe/brzegi trójkąta: a(n,0)=1 dla n≥0 a(1,1)=1 a(n,n)=0 dla n≥2 I teraz najważniejsze, czyli dostrzeżenie rekurencji: a(n,k)=a(n−1,k)+a(n−2,k−1) dla n≥3, 1<k<n Objaśnienie: element największy ze zbioru n−elementowego albo należy do podzbioru k−elementowego, albo do niego nie należy. Takich podzbiorów (spełniających warunki o braku elementów sąsiednich) nie zawierających tego maksymalnego elementu jest oczywiście a(n−1,k). Jeśli natomiast ów element maksymalny należy do podzbioru, to element "przedmaksymalny" (przedostatni przed maksymalnym) do tego podzbioru należeć nie może, a zatem pozostałe (k−1) elementów tego podzbioru spełniających warunki o niesąsiadowaniu należy wybrać z (n−2) najmniejszych elementów w zbiorze, czyli na a(n−2,k−1) sposobów. Po narysowaniu tego trójkąta łatwo dostrzec, że:

	n−k+1 k		n+1
a(n,k)=		dla k≥0, n≥0, n−k+1≥k, czyli dla n≥0, 0≤k≤
			2

a(n,k)=0 dla pozostałych k, n

xxx: Dziekuje. Zadanie 4 w twoim rozumowaniu jest sluszne czy jc mial racje?

Pytający: 4. Jest źle policzone, mój błąd. Faktycznie nie wszystkie możliwości uwzględniłem, bo poprawne rozsadzenie może powstać również poprzez odpowiednie dosadzenie n−tej pary do niepoprawnego rozsadzenia (n−1) par (o ile maksymalnie 2 pary siedzą obok siebie). Przykładowo z ustawienia AABB dla n=2 może powstać ACABCB dla n=3 i tego nie uwzględniłem. jc, czyli ani 24, ani 192. Wszystkich możliwych ustawień jest (6−1)!=120.

Pytający: 4. Poprawione: |żadna para obok siebie|=|wszystkie ustawienia|−|przynajmniej jedna para obok siebie| |wszystkie ustawienia|=(2n−1)! Z zasady włączeń i wyłączeń:

	n k
|przynajmniej jedna para obok siebie|=∑k=1n((−1)k*		*((2n−k)−1)!*2k)

(−1)^k // z zasady włączeń i wyłączeń

n k
	// wybór k par, które na pewno siedzą obok siebie

((2n−k)−1)! // wybrane wyżej pary traktujemy jako 1 element, więc mamy (2n−k) elementów do rozsadzania wokół stołu 2^k // w każdej z wybranych par siedzących obok siebie możemy zamienić miejsca Zatem: a₁=0

	n k
an=∑k=0n((−1)k*		*((2n−k)−1)!*2k) dla n≥2

// a₃=32

jc: W przypadku ławy mielibyśmy

	n 1		n 2
(2n)! −		(2n−1)! +		(2n−2)! − ...

n=2, 4! − 2*3! 2 + 2! 4 = 24−24+2*4= 8 n=3, 6! − 3*5! 2 + 3*4! 4 − 3! 8 = 720 − 720 + 288 − 48 = 240 Jednak w przypadku okrągłego stołu jest mniej możliwości.

jc: We wzorze powyżej zapomniałem dopisać 2^k.

	n 1		n 2
bn=(2n)! −		(2n−1)! 2 +		(2n−2)! 22 − ...

A jak przejść od ławy do stołu okrągłego? Może odjąć to, czego nie uwzględniliśmy (na końcu i na początku siedzi mąż i żona). a_n=b_n−2n b_n−1 ? b₀=1 b₁=0 b₂=8 b₃=240 a₁=0 a₂=8−0=8 a₃=240−2*3*8=192 ?

jc: Mam tez taki wzór: a_n = (w_n − w_n−1) n! 2ⁿ w₀=1 w₁=0 w_n+1=(2n+1) w_n + w_n−1 Kolejno: 1, 0, 1, 5, 36, 329 Różnice: 1, 0,1, 4, 31, 293 Iloczyny: 1, 0, 8, 4*8*3! = 192, 31*16*4!=11904 Tylko czy to jest dobrze?

Mila: (1) To zmienia postać rzeczy: Podstawiam (odszukaj wiersz )

	1		1
A(x)=a0+a1*x+a2*x2+		x3*A(x)+x2*(A(x)−a0)−		x*(A(x)−a0−a1x)=
	2		2

	1		1		1		1
=1+x+x2+		x3*A(a)+x2*A(x)−x2−		x*A(x)+		x+		x2⇔
	2		2		2		2

	1		1		1		3
A(x)−		x3*A(x)−x2*A(x)+		x*A(x)=		x2+		x+1
	2		2		2		2

	1		1		1		3
A(x)*(−		x3−x2+		x+1)=		x2+		x+1⇔
	2		2		2		2

	1   3   x2+ x+1 2   2
A(x)=
	1   1   (− x3−x2+ x+1)   2   2

	0.5*(x+1)*(x+2)
A(x)=
	1   − *(x−1)(x+1)*(x+2)   2

	1
A(x)=
	1−x

a_n=1 ciąg stały. II sposób 1)równanie charakterystyczne 2) jawna postać ciągu ( można ustalic na piechotę licząc kilka wyrazów, ale bez warunków początkowych liczyłam tradycyjnie) a_n=1 3)

	1
A(x)=
	1−x

Xxx: Dziękuję wszystkim. Jesteście wspaniali

Mila: Na drugi raz wcześniej zacznij przygotowywać się do zajęć

Pytający: jc, licząc a_n=b_n−2n*b_n−1 nie uwzględniasz, że otrzymujesz wiele ciągów oznaczających to samo ustawienie. Zobrazuję dla n=3: • ABCABC CABCAB BCABCA odpowiadają jednemu ustawieniu (z dokładnością do zamian w parach). Ponadto zamiana A niczego tu nie zmienia (bo po obu A występuje to samo: BC).

	24
U Ciebie jest to policzone 23*3=24 razy. Dla okrągłego stołu mamy		=4 takie
	2*3

ustawienia: A₁B₁C₁A₂B₂C₂ A₁B₁C₂A₂B₂C₁ A₁B₂C₁A₂B₁C₂ A₁B₂C₂A₂B₁C₁ • analogicznie jest dla: ACBACB // przesunięć cyklicznych już nie wypisuję

	24
U Ciebie jest to policzone 23*3=24 razy. Dla okrągłego stołu mamy		=4.
	2*3

W poniższych przypadkach zamiana A już robi różnicę, ale mamy też u Ciebie 6*2³ różnych ciągów w każdym przypadku (bo co innego jest po obu A): • ABACBC CABACB BCABAC CBCABA ACBCAB BACBCA

	48
U Ciebie jest to policzone 23*6=48 razy. Dla okrągłego stołu mamy		=8.
	6

• ACABCB // przesunięć cyklicznych już nie wypisuję

	48
U Ciebie jest to policzone 23*6=48 razy. Dla okrągłego stołu mamy		=8.
	6

• ABCACB // przesunięć cyklicznych już nie wypisuję

	48
U Ciebie jest to policzone 23*6=48 razy. Dla okrągłego stołu mamy		=8.
	6

Łącznie tych (2*3+3*6)*2³=192 ciągów odpowiada 2*4+3*8=32 różnym rozsadzeniom wokół stołu.

Pytający: I warto pisać zadania w oddzielnych wątkach, bo mały śmietnik się robi.

jc: Pytający, U mnie miejsca są ponumerowane. Rozumiem, że u Ciebie ważne jest jedynie sąsiedztwo (kto siedzi po prawej, kto po lewej). Jeśli dla n=3 masz wynik 32, to znaczy, że w zasadzie mamy to samo. http://oeis.org/search?q=0%2C2%2C32%2C1488&sort=&language=english&go=Search

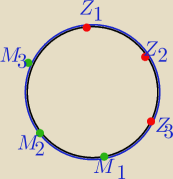
Mila: A tak mogą siedzieć?

jc: Sprawdziłem, kolejna liczba też się zgadza.

Mila: Też myślę jak rozwiązać. Ile macie możliwości dla 3 par?

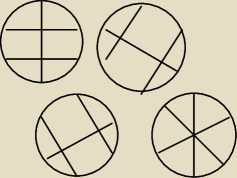
jc: A dlaczego nie?

jc: Jeśli numerujemy miejsca: 192, jeśli patrzymy tylko na sąsiadów: 32.

Pytający: Wydaje mi się, że jeśli miejsca miałyby być rozróżnialne, to byłoby to wspomniane w zadaniu, ale kto wie, może o rozróżnialne chodziło. I fakt, jest dobrze, jeśli: a_n // sposobów dla miejsc rozróżnialnych b_n // sposobów dla miejsc nierozróżnialnych to: a_n=2n*b_n.

Mila: To mi się zgadza dla 3 par, gdy miejsca nie są numerowane, ważni są sąsiedzi. Niestety nie mogę zrozumieć linka z 23:19. Jutro znajdę stronę z tłumaczeniem. Dobranoc

jc: Po prostu wklikałem kilka początkowych wyrazów do encyklopedii i na pierwszym miejscu pojawił się problem z okrągłym stołem.

jc: Mila, widziałem kiedyś to zadanie w książce Halla, gdzieś na początku. Mam kopię książki, ale niestety zaczyna się od połowy. Czyżbym początek uznał za niepotrzebny?