trapez
planimetria:
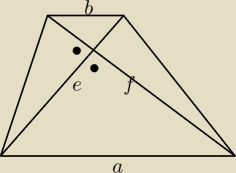
Przekatne są prostopadłe
Mam wykazać że f
2+e
2=(a+b)
2
21 cze 00:41
Basia:
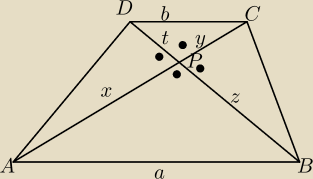
| | a | |
trójkąty APB i CPD są podobne w skali k = |
| |
| | b | |
stąd:
x = ky
z = kt
e
2+f
2 = (x+y)
2+(z+t)
2 = (ky+y)
2+(kt+t)
2 =
y
2(k+1)
2+t
2(k+1)
2 = (k+1)
2(y
2+t
2) =
| | a | | a2 | | a | |
( |
| +1)2*b2 = ( |
| +2* |
| *1+1)*b2 = |
| | b | | b2 | | b | |
a
2+2ab+b
2=(a+b)
2
21 cze 00:57
PW: Skorzystać z podobieństwa trójkątów o bokach a,f1,e1 i b, f2,e2 i twierdzenia Pitagorasa.
21 cze 00:57
Eta:
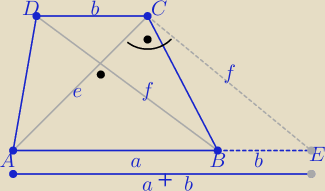
Z tw. Pitagorasa w ΔAEC
f
2+e
2=(a+b)
2
=============
c.n.w.
21 cze 01:23