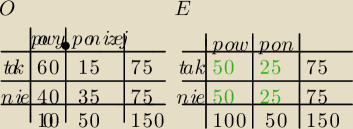hipoteza wiewiór: zapytano 150 losowo wybranych osób, czy ich wynagrodzenie jest powyżej czy poniżej średniej krajowej oraz czy są szczęśliwi. Wyniki zamieszczono w tabeli. Zweryfikować hipotezę statystyczną. Postępować według kroków. a)hipotezy b)statystyka testowa c)obliczona statystyka d)P−wartość e)decyzja wynagrodzenie powyżej poniżej szczęśliwy tak 60 15 nie 40 35

Jack: to typowy test chi kwadrat na niezależność H₀: wynagrodzenie i szczęśliwość są od siebie niezależne (czyli na polski − wynagrodzenie nie wpływa na to czy ktoś jest szczęśliwy czy nie) H₁: − | | − są od siebie zależne. Ta tabelka co otrzymaliśmy to jest tabelka O (obtained−otrzymane) Należy dopisać jeszcze sumy poszczególnych kolumn i wierszy. np. kolumna1 −> 60+40 = 100, oraz sumę ostateczna tak żeby wyszedł rozmiar próby tzn. suma ostatniego wiersza = suma ostatniej kolumny = 150 (w tym wypadku) Musimy zrobić teraz tabelkę E (expectations − czyli w sumie tego czego się spodziewamy) najpierw przepisujemy sumy wierszy i kolumn (tzn. ostatni wiersz i ostatnia kolumna z tabelki O, a następnie liczymy wartości w środku w ten sposób, ze: np. przecięcie:

	75*100
tak−powyżej −−−−−>		= 50
	150

czyli mnożymy odpowiednio ostatnia kolumna * ostatni wiersz / ilość obserwacji zatem kolejne:

	50*75
tak − poniżej −−−−−>		= 25
	150

	75*100
nie − powyżej −−−−−>		= 50
	150

	75*50
nie − poniżej −−−−>		= 25
	150

Wartosc statystki chi kwadrat to jest suma po wszystkich elementach

	(O−E)2
tych w środku: ∑
	E

zatem

	(50−60)2		(25−15)2		(50−40)2		(25−35)2
χ2 =		+		+		+		= ...
	50		25		50		25

ilość stopni swobody: df = (liczba kolumn−1) * (liczba wierszy −1) = (2−1)*(2−1) = 1 mówimy oczywiście o tych kolumnach i wierszach z wartościami, bez nagłówków i sum Teraz wystarczy sprawdzić p−wartość dla df=1 oraz przyjętego α. Zazwyczaj α=0.05 jeżeli 2 * p−wartość < χ² to odrzucamy H₀. Jako, że jest to test dwustronny (to mamy 2*pwartość), dla jednostronnego byłoby 1*p−wartość)