p Kamil: Wierzchołkami grafu G są wierzchołki sześcianu, a krawędziami− krawędzie dwóch równoległych ścian oraz cztery przekątne sześcianu. Zbadaj, czy to graf planarny. Czyli powyższy graf ma |V|=8 każdy wierzchołek jest stopnia 3, więc |E|=12. nie wiem jak to udowodnić. Ten graf spełnia wszystkie nierówności typu |E|≤3|V|−6 oraz |E|≤2|V|−4 Można także pokolorować wierzchołki kolorami "A" oraz "B", aby sąsiadujące wierzchołki miały inne kolory, oraz tych kolorów jest równa ilość. Tylko jak graf spełnia te zależności, to nie potwierdza że jest planarny prawda?

Kamil: up

Kamil: Aż takie trudne zadanie?

jc: Opisany obiekt uzyskasz obracając jedną ścianę sześcianu o 180 stopni. Zatem jest to graf planarny.

Kamil: Ok. A jeśli nie wpadnę na pomysl jak to narysować. To jak można udowodnić że jest planarny?

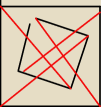
jc: A teraz sobie pomyśl co uzyskasz obracając środkowy kwadrat. Oczekujesz automatycznej procedury, która da dowód?

Kamil: Nie, ale musi być też inny sposób, przynajmniej moim zdaniem, bo nie zawsze jest się w stanie narysować graf(np z 50 wierzchołkami) i sprawdzenia czy jest planarny graficzną metodą.

jc: Są takie gry, gdzie przesuwasz wierzchołki aż uzyskasz graf planarny. Program tego rodzaju ułatwiłby przesuwanie wierzchołków. Wydaje się, że można by to zautomatyzować: każde przesunięcie zmniejszałoby liczbę przecięć. Ale mogę się mylić, może po drodze czasem trzeba zwiększyć liczbę przecięć? http://johntantalo.com/wiki/Planarity/

Pytający: Są sposoby, ale "ręcznie" raczej nie będziesz sprawdzał: https://en.wikipedia.org/wiki/Planarity_testing http://jgaa.info/accepted/2004/BoyerMyrvold2004.8.3.pdf