sadasd
das: Jak narysować na płaszczyźnie zespolonej?
|z + 2π| ≤ 2π
Rozbijam na dwie
z+2π≤−2π
z≤−4π
x ≤ −4π
y ≤ 0
z+2π ≤ 2π
z ≤ 0
x ≤0
y≤0
i cześć wspólna przedziałów?
Wydaje mi się, że źle, proszę o pomoc

20 cze 16:49
das: Może tak:
√(x +2π)2 + y2≤2π
20 cze 17:00
Mila:
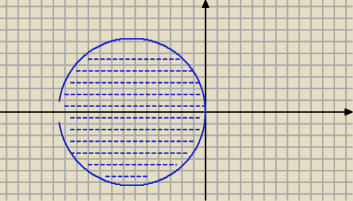
1)
|z−(−2π)|≤2π
koło o środku (−2π,0) i r=2π
Albo tak
2)
z=x+iy, x,y∊R
|x+iy+2π|≤2π
|(x+2π)+iy|≤2π
√(x+2π)2+y2≤2π /
2
(x+2π)
2+y
2≤4π
2
koło o środku (−2π,0) i r=2π
20 cze 17:16
20 cze 17:26
das: Dziękuje Mila

20 cze 17:27
das: Mam jeszcze takie coś
|z + 2π| ≤ −arg(z + 2π)
|z − ( −2π)| ≤ −arg(z + 2π)
Mam pytanie, czy mogę przedstawić 2π jako −1? (z postaci trygonometrycznej)
20 cze 17:39
the foxi:
Wolfram potraktował z jako zmienną rzeczywistą a nie zespoloną

20 cze 19:31
Adamm:
To będzie spirala Archimedesa
20 cze 19:35
Adamm:
Właściwie to nie będzie
argument jest nieujemny bo z przedziału [0, 2π)
więc musi być x=−2π
20 cze 19:37
das: Pomyślę potem jeszcze i dam znać czy rozumiem, na tę chwilę dziękuje
20 cze 19:56
das: @Adamm umiesz to narysować?
Jedynie co mi się nasuwa to początek spirali w (−2π, 0)..
A no właśnie nie spirali tylko bym narysował w drugą stronę, tzn. ze wskazówkami zegara. Tylko
co z tym 2π w argumencie?
20 cze 21:07

 1)
|z−(−2π)|≤2π
koło o środku (−2π,0) i r=2π
Albo tak
2)
z=x+iy, x,y∊R
|x+iy+2π|≤2π
|(x+2π)+iy|≤2π
√(x+2π)2+y2≤2π /2
(x+2π)2+y2≤4π2
koło o środku (−2π,0) i r=2π
1)
|z−(−2π)|≤2π
koło o środku (−2π,0) i r=2π
Albo tak
2)
z=x+iy, x,y∊R
|x+iy+2π|≤2π
|(x+2π)+iy|≤2π
√(x+2π)2+y2≤2π /2
(x+2π)2+y2≤4π2
koło o środku (−2π,0) i r=2π

