dadas das: Rysowanie na płaszczyźnie zespolonej:

	3π
arg ( z − 1 − 2i) =
	2

Nad z jeszcze jest kreska ( z sprzężone − nie umiem tego napisać) Jak sobie z tym poradzić? Gdyby nie było sprzężone to bym narysował

	3π
arg(z − (1 + 2i) =
	2

Ale z tym sprzężeniem nie wiem jak

Adamm: zastanów się co robi ze zmienną z sprzężenie jakie to jest przekształcenie płaszczyzny

das: Liczby zespolone odbija symetrycznie względem osi rzeczywistej?

das: Zgadza się z odpowiedzią. Jest to półprosta?

das: Kąt również się zmienia?

Adamm: narysuj arg(z−(1+2i))=3π/2 oznaczmy sobie to równanie T(z) masz zbiór {z∊C : T(z) }={ z^*∊C : T(z^*) } teraz jeśli sprzężymy każdy element należący do tego zbioru, to otrzymamy zbiór { (z^*)^*∊C : T(z^*) } = { z∊C : T(z^*) } czyli to co chcieliśmy czyli wystarcza narysować punkty spełniające T(z), i wtedy wszystko odbić względem osi rzeczywistej

Mila:

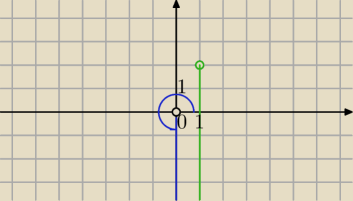
	3π
Półprosta niebieska to zbiór {z: arg(z)=		}
	2

	3π
Półprosta zielona to zbiór {z: arg(z−(1+2i))=		}
	2

dalej w następnym wpisie

Mila:

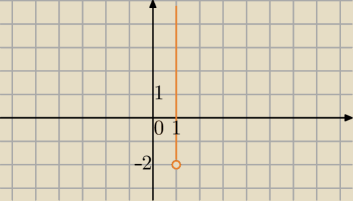
	3π
Półprosta żółta to zbiór {z: arg(z*−(1+2i))=
	2