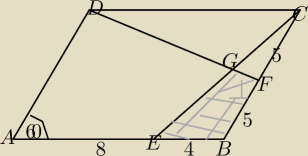
Mam obliczyć pole EBFG
Pomoże ktoś 
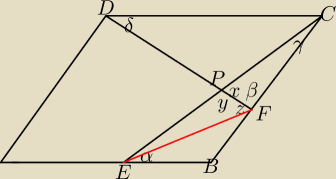z tw.cosunusów można policzyć EC i potem z tw.sinusów wyznaczyć kąty α=<BEC i γ=BCE
analogicznie FD i kąty β i δ
gdy masz β i γ to masz x
z tw.sinusów wyliczasz PF i PC
PE = EC−PC
y=180−x
PEBFP = PEBF+P{EPF}
strasznie dużo liczenia; można pomyśleć nad prostszym rozwiązaniem
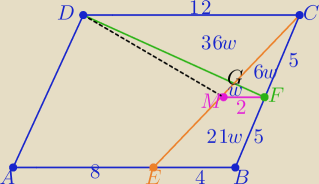Można też tak:
Z podobieństwa trójkątów MFC i ABC |MF|=2
i w trapezie MFCD pola trójkatów : w, 6w, 36w
P(ΔEBC)=7w*22=28w to P(EBEM)= 21w
więc P(EBFG)=22w
| 1 | 5√3 | |||
P(ΔDFC)=42w= | *12*5*sin60o ⇒ w= | |||
| 2 | 14 |
| 65√3 | ||
zatem P(EBFG)=22w = | ||
| 7 |
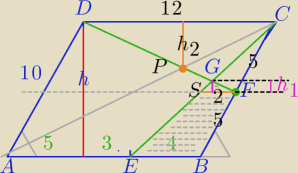1) h=5√3,
PEBFG=PEBFS+PΔSFG
2)|SF|=2
| 2+4 | 5√3 | 15√3 | ||||
PEBFS= | * | = | ||||
| 2 | 2 | 2 |
| 2 | 1 | |||
3) ΔSFG∼ΔDCF w skali k= | = | |||
| 12 | 6 |
| 1 | 5√3 | |||
7x= | h⇔7x= | |||
| 2 | 2 |
| 5√3 | ||
x= | =h1 | |
| 14 |
| 1 | 5√3 | 5√3 | ||||
4) PΔSFG= | *2* | = | ||||
| 2 | 14 | 14 |
| 15√3 | 5√3 | |||
5)PEBFG= | + | |||
| 2 | 14 |
| 55√3 | ||
PEBFG= | ||
| 7 |
| 22*5√3 | 55√3 | |||
to ja mam literówkę.... 22w= | = | |||
| 14 | 7 |