s Kamil: Niech G będzie wielościanem (lub grafem wielościanu), którego każda ściana jest pięciokątem lub sześciokątem. Udowodnić, że G ma co najmniej 12 ścian pięciokątnych. x−ilość ścian pięciokątnych y−ilość ścian sześciokątnych s=|E|+2−|V| |E|≤3|V|−6 s=x+y

	5x+6y
|E|=
	2

5x+6y		5x+6y
	≤3|V|−6 →|V|≥		+2
2		6

na ten moment dobrze?

Kamil: znalazłem takie rozwiązanie. skąd wzięła się ta nierówność? zaznaczyłem w kółko https://image.ibb.co/eodcjd/Przechwytywanie.png

jc: s=x+y 2k=5x+6x 2k ≥ 3w 2=w−k+s x=6s−2k 12=6w−6k+6s≤4k−6k+6s=6s−2k=x

jc: Jedyna nierówność to 2k≥3w wynika założenia, że z każdego wierzchołka wychodzą co najmniej 3 krawędzie.

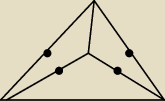
jc: Gdyby stopnie mogły być niższe niż 3, to moglibyśmy narysować coś takiego (4 pięciokąty).