wykazywanie mati: W trójkącie równobocznym ABC poprowadzono prostą k która przecina bok BC w punkcieD pod kątem 15⁰ a bok AB w punkcie E Prosta ta dzieli trójkąt ABC na dwie figury których pola są w stosunku 1:5 Wykaż ,że |BD|+|BE|=|AB|

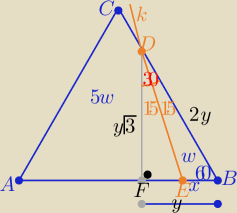
Eta: Moja propozycja Trójkąt FBD "ekierka" o kątach 60^o,30^o,90^o i odpowiednie oznaczenia

	a2√3		1		xy√3		a2
P(ABC)=6w ⇒ w=		i w=		*2y*x*sin60o ⇒ w=		to 2y=
	24		2		2		6x

Z tw. o dwusiecznej (k) w ΔFBD

y√3		y−x		√3		y
	=		⇒		=		−1 ⇒ 2y=x(√3+2)
2y		x		2		x

	a2
zatem		= x(√3+2)
	6x

to a²=6x²(√3+2) ============ Mamy wykazać,że 2y+x=a x(√3+2)+x=a ⇒x(√3+3) =a to a²=[x(√3+3)]² ⇒a² x²(12+6√3) a² = 6x²(√3+2) ============= zatem taka równość zachodzi c.n.w

mati: Dziękuję Eta