2 zadanka yung kiki: 1. Pole trapezu równoramiennego o kącie przy podstawie 60° jest równe 2√3. Wyznacz wymiary trapezu o najmiejszym obwodzie. Uzasadnij, ze w trapez ten mozna wpisać okrąg i oblicz promień tego okręgu. 2. Kąt przy wierzchołku A rownoległoboku ABCD jest równy α, s krótsza przekątna jest prostopadła do boków AB i CD. Objętość powstałej bryły przez obrót równoległoboku wokół boku AB jest rowna V. Wyznacz pole powierzchni tej bryły.

Eta:

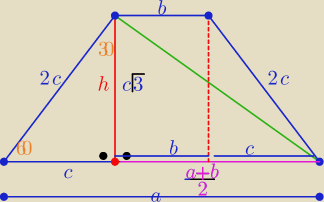
	a+b		4
P=		*h ⇒ (b+c)*c√3=2√3 ⇒ (b+c)*c=2⇒ (a+b)*c=4⇒ a+b=
	2		c

	4
Obwód L =a+b+4c ⇒ L(c)=4c+
	c

	4		4c2−4
L'(c)=4−		=		⇒L'(c)=0 ⇒ c=1
	c2		c2

Zbadaj znak pochodnej ..... zatem dla c=1 obwód jest najmniejszy to trapez ma wymiary: 2c=2 , b=1, a=3 warunek wpisania okręgu w trapez a+b=2c+2c ⇒ 4=4 zatem w taki trapez można wpisać okrąg

	√3
2r=h ⇒ r=
	2

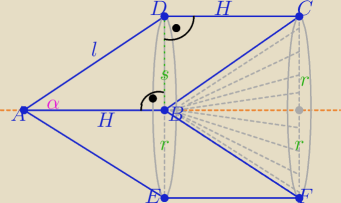
Eta: r=s V(bryły) = V walca(EFCD) =πr²*H ( bo stożki doklejony i wydrążony są przystające więc mają równe objętości i równe pola powierzchni P_c(bryły)= P_b(walca)+2P_b(stożków W ΔABD:

	s
l=		i H=s*ctgα
	sinα

V=πs²*H=.................. P_c= 2πsH+2πsl= ......................... dokończ obliczenia

Mila: Właśnie Eto zostawiłam dla Ciebie Konfiturki zrobione?

yung kiki: dziękuję bardzo