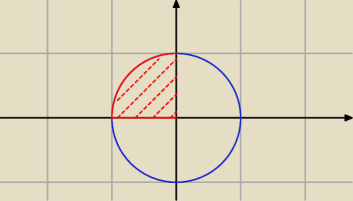
Całka podwójna pomocy! hesio: Naszkicować obszar D i obliczyć całkę ∬y²dxdy gdy D: x²+y²≤1 i x≤0 y≥0 dokonując zamiany na współrzędne biegunowe. Kompletnie nie wiem jak to zrobić...

piotr:

	π
∫π/2π∫01 r3 sin2(φ) dr dφ =
	16

hesio: wszystko się zgadza, lecz nie rozumiem rozwiązania tej całki. Mógłbyś wytłumaczyć?

jc: Na czym polega rozwiązanie całki?

Jerzy: We współrzędnych biegunowych : y = rsinφ i jeszcze musisz pomnożyć przez tzw Jakobian: r

hesio: w momencie podstawienia się gubie

piotr: mamy iloczyn dwu całek ∫_π/2^πsin²φ dφ ∫₀¹r³ dr

	φ		1		π
∫π/2πsin2φ dφ =		−		sin(2φ)|π/2π =
	2		4		4

	r4		1
∫01r3 dr =		|01 =
	4		4