wzor? Krystek: Niech G bedzie grafem planarnym w ktorym kazfy wierzcholek ma stopien 3 Pokazac ze jezeli G ma plaska reprezentacje w ktorej kazdy region jest ograniczony czterema lub szescioma krawedziami to istnieje dokladnie szesc regionow ograniczonych czterema krawedziami wiec x−liczba scian ograniczona czterema krawedziami y−liczba scian ograniczona szesioma krawedziami |E|=(4x+6y)/2 |V|=(4x+6y)/3−nwm kompletnie skad ten wzor,dlaczego na 3 dzielimy,ten wzor jest poprawny bo robilismy to na zajeciach ,ale nwm skad to się wzieło?

jc: s=x+y 2k=4x+6y 3w=2k z każdego wierzchołka wychodzą 3 krawędzie w−k+s=2 wzór Eulera x= 3(x+y)−(2x+3y)=3s−k=3(2−w+k)−k=6−3w+2k=6

Krystek: ok,a jak bym nie mial w treści zadania ze kazdy wierzcholek ma stopien 3?

jc: To liczba czworokątów mogłaby być dowolnie duża.

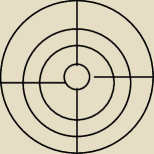
jc: 14 czworokątów

Krystek: ok,thx