Rachunek prawdopodobieństwa Ania: 1. Zakończenie budowy może zostać opóznione przez strajk. Prawdopodobieństwo strajku wynosi 0,60. Prawdopodobieństwo, że budowa zostanie zakończona w terminie, gdy nie będzie strajku, wynosi 0,85. Prawdopodobieństwo, że budowa zostanie zakończona w terminie, gdy będzie strajk, wynosi 0,35. a) Jakie jest prawdopodobieństwo, że budowa zostanie zakończona w terminie? b) Przypuśćmy, że budowa została zakończona w terminie. Jakie jest prawdopodobieństwo, że był strajk? a) 0,85 + 0,35 − 0,60 = 0,60 b) 0,35 2. Pracownicy pewnej firmy doradczej wynajmują samochody w trzech wypożyczalniach samochodów: 60% z wypożyczalni 1., 30% z wypożyczalni 2. i 10% z wypożyczalni 3. Wiadomo, że 9% samochodów z wypożyczalni 1. wymaga naprawy, 20% samochodów z wypożyczalni 2. wymaga naprawy i 6% samochodów z wypożyczalni 3. wymaga naprawy. Okazało się, że pewien samochód wymaga naprawy. Jakie jest prawdopodobieństwo, że pochodzi z wypożyczalni 2.? 9/60 * 2/30 * 6/10 = 216, wynik − 21,6% 3. Wiadomo, że w województwie pomorskim 8% osób powyżej 50. roku życia ma cukrzycę. Służba zdrowia w województwie pomorskim rozpoznaje cukrzycę poprawnie u 95% osób (tzn. u osób, które mają cukrzycę) i rozpoznaje cukrzycę niepoprawnie u 2% osób (tzn. u osób, które jej nie posiadają). Jakie jest prawdopodobieństwo, że a) służba zdrowia w województwie pomorskim rozpozna cukrzycę u osoby powyżej 50. roku życia; b) osoba powyżej 50. roku życia ma cukrzycę, jeżeli służba zdrowia rozpozna u niej tę chorobę? a) 95 − 2 = 93 b) po prostu 95? Dobrze zrobiłam te zadania? Jeśli gdzieś jest źle to prosiłabym z wyjaśnieniem Dziękuje z góry za pomoc

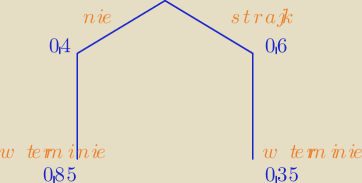
iteRacj@: zad.1 a/ skorzystaj z 'drzewka' i spróbuj poprawić

Ania: 1. a) 0,35 * 0,6 + 0,85 * 0,4 = 0,21 + 0,34 = 0,55 0,35* 0,6/(0,55) = 0,21/0,55 = 0.38 jest ok?

iteRacj@: ok

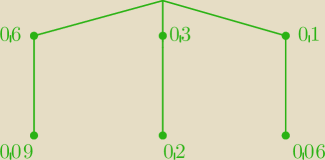
iteRacj@: zad.2 popraw w taki sam sposób

Ania: 2. (0,2 * 0,3)/0,9*0,6+0,2*0,3+0,1*0,06 = 0,06/0,12 = 0,5?

iteRacj@: tak jest, zad.trzecie też do poprawienia

Ania: 3. a) 0,95 * 0,02 = 0,019 −− 1,9%? b) 0,95 * 0,08 = 0,076 1 − 0,76 = 24 −− 24%? dobrze?

Ania: Czy w 3. b) bez tego odejmowania i po prostu 76%?

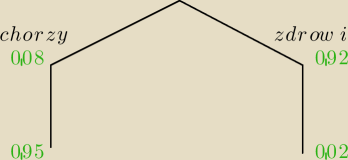
iteRacj@: Z treści zadania wynika, że "służba zdrowia pomorskim rozpozna cukrzycę" oznacza pozytywny wynik testu czy badania i nie musi oznaczać choroby, chodzi tylko o rozpoznanie. Te prawdopodobieństwa rozpoznania są na rysunku.

Ania: czyli b) 8 − 1,9 = 6,1% ma rozpoznaną chorobę z tych 8%? na podpunkt a nie mam pomysłu

iteRacj@: a/ prawdopodobieństwo, że służba zdrowia w województwie pomorskim rozpozna cukrzycę 0.08*0,95 + 0.92*0,02 = 0,0944 to są rozpoznania u tych zdrowych i u chorych w sumie

Ania: aa ok już rozumiem A podpunkt b jest dobrze?

iteRacj@: b/ P(R) = 0,0944 − prawdopodobieństwo, że służba zdrowia rozpozna u kogoś cukrzycę P(C) − prawdopodobieństwo, że mieszkaniec województwa jest chory na cukrzycę P(C∩R) = 0,95 − prawdopodobieństwo, że badany jest chory cukrzycę i rozpoznano u niego chorobę P(C|R) − prawdopodobieństwo, że badany jest rzeczywiście chory na cukrzycę pod warunkiem, że jest osobą, u której rozpoznano chorobę

	P(C∩R)
P(C|R)=
	P(R)

iteRacj@: to jest ten sam wzór na prawdopodobieństwo warunkowe i ten sam schemat liczenia, co w poprzednich zadaniach