prosze o pomoc Ania: Bardzo proszę o pomoc Dany jest graniastosłup prawidłowy sześciokątny, którego wysokość ma długość 12, a krawędź podstawy długość 5. Zakładamy, że wylosowanie każdego z 12 wierzchołków tego graniastosłupa jest jednakowo prawdopodobne. Losujemy dwa różne wierzchołki. Niech A oznacza zdarzenie: "odległość wylosowanych wierzchołków jest liczbą naturalną", B zdarzenie: "wylosowane wierzchołki należą do tej samej podstawy". P(A), P(B) = ?

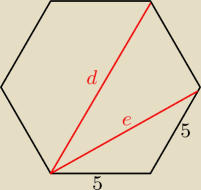
Basia: Oblicz najpierw długość odcinków d,e. Podaj wyniki.

Ania: d = 10, a nie wiem jak e obliczyc

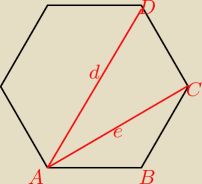
Basia: a ile stopni ma kąt ACD ?

Ania: 90? czyli e to √75?

Basia: tak; √75=√25*3 = 5√3 teraz policz długości przekątnych graniastosłupa; też masz dwie możlowości to będą trójkąty d,H,D i e,H,E D² = d²+H² = 10²+12² = 100+144=244 = 2*122=2*2*61 D = 2√61 E² = e²+H²=75+144=219=3*73 E = √219=√3*√73 długość D i E są liczbami niewymiernymi cd. za chwilkę

Ania: dobrze

Basia: |Ω| = 12*11 A − odległość jest liczbą naturalną pierwszy wierzchołek dowolnie czyli 12 możliwości drugi musi być: − sąsiedni po krawędzi podstawy (2 możliwości) − po przekątnej d (1 możliwość) − sąsiedni po krawędzi bocznej (1 możliwość) czyli razem 4 |A| = 12*4 P(A) = ^12*4_12*11 = ⁴₁₁ B − należą do tej samej podstawy pierwszy dowolnie czyli 12 drugi na 5 sposobów razem 12*5 P(B) = ^12*5_12*11 = ⁵₁₁ −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− można też podejść do tego inaczej

	12 2
|Ω|=

|B| jest łatwo wyliczyć

	6 2
|B| = 2*

wynik jest identyczny natomiast przy tym podejściu trudniej wyliczyć |A| w każdym razie ja się nie podejmuję

Basia: E tam! Za szybko odpuściłam. Liczymy tak samo jak przy pierwszym podejściu i dzielimy przez 2!=2 (bo każdy został policzony dwukrotnie AB=BA itd) wyjdzie to samo bo musi

Ania: a dlaczego moc omegi to 12 razy 11, moc A 12 razy 4 i B 12 razy 5? PROSZE O WYTŁUMACZENIE

Basia: pierwszy wierzchołek mogę wybrać dowolnie; jest ich 12 czyli 12 możlowości drugi już tylko na 11 sposobów |Ω| to 12*11 bo biorę "każdy z każdym" A znowu pierwszy jest dowolny czyli 12 dla każdego z tych 12 mogę dopasować 4 inne i znowu "każdy z każdym" czyli |A| = 12*4 B znowu pierwszy jest dowolny czyli 12 drugi ma być w tej samej podstawie czyli zostało mi 5 do wyboru stąd 12*5