Oblicz wysokość w prostopadłościanie.
hipo: Proszę o rozwiązanie zadania ze zbioru zadań dla asa
"Z Pitagorasem przez gimnazjum" (klasa 3 gimnazjum):
W prostopadłościanie ABCDA₁B₁C₁D₁ poprowadzono płaszczyznę ACD₁,
która tworzy z podstawą ABCD kąt α = 60°.
Oblicz pole powierzchni całkowitej i objętość prostopadłościanu,
jeżeli |AB| = 8 cm, |BC| = 6 cm.
13 cze 14:11
sushi:
polecenie było, że czeka na gotowca, a tu będzie wieczorem niespodzianka −> zadanie
nierozwiązane w 100%
13 cze 17:09
hipo:
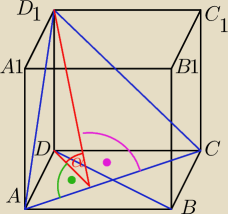
@Mila
Czy kąt α nie jest pomiędzy wysokościami trójkątów ACD i ACD1?
Niestety, nie jestem gimnazjalistą.
13 cze 23:27
hipo: @sushi
Tak, tak .. na 100% → matematyczne myślenie.
13 cze 23:30
PW: Kąt między dwiema przecinającymi się płaszczyznami mierzy się na płaszczyźnie prostopadłej do
ich wspólnej krawędzi (taka jest definicja).
Należy więc wziąć płaszczyznę prostopadłą do AC i na niej mierzyć kąt.
13 cze 23:50
Mila:
Oj , tak. Δ nie jest równoramienny, tak to jest, gdy robię zadanie między konfiturą a torcikiem
dla jutrzejszych gości

zrobisz, czy mam rozwiązać?
13 cze 23:52
hipo: @Mila @PW
Dziękuję za pomoc. Już wcześniej zrobiłem tylko zastanawiam się który to kąt.
W odpowiedzi jest: V = 240√3 czyli, że H=5√3.
14 cze 00:02
Mila:
Kąt masz dobry na rysunku, ale wynik to wg mojego błędnego rysunku.
14 cze 00:25
Mila:
Jutro napiszę.
Dobranoc

14 cze 00:28
Mila:
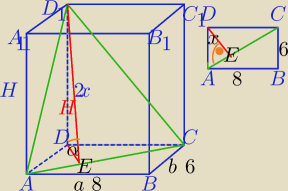
α=60
o, |DE|=x −wysokość ΔADC poprowadzona do przeciwprostokątnej
1)
W ΔADC:
|AC|
2=8
2+6
2
|AC|=10
2) ΔDEC− Δ 90,60,30
Przeciwprostokątna |EC|=2x
3) W ΔD
1DE: | D
1E|
2=|DE|
2+H
2
(2x)
2=H
2+x
2
H
2=4x
2−x
2
H
2=3x
2
=============
4) obliczyć wg wzorów
Mam nadzieję, że nie ma błędów w rachunkach
Eto sprawdź! Proszę.
14 cze 00:31
hipo: Taki jest też wynik w odpowiedziach zbioru zadań. Wysokość trójkąta ACD wynosi 4,8 cm,
zatem wysokość prostopadłościanu to 4,8√3 cm a objętość V = 230,4√3 cm3.
Smacznego życzę i dobranoc.
14 cze 00:41
hipo: @Eto
Nie ma błędów. Dziękuję za pomoc.
14 cze 00:45
utem:
14 cze 15:15
 @Mila
Czy kąt α nie jest pomiędzy wysokościami trójkątów ACD i ACD1?
Niestety, nie jestem gimnazjalistą.
@Mila
Czy kąt α nie jest pomiędzy wysokościami trójkątów ACD i ACD1?
Niestety, nie jestem gimnazjalistą.
 zrobisz, czy mam rozwiązać?
zrobisz, czy mam rozwiązać?

 α=60o, |DE|=x −wysokość ΔADC poprowadzona do przeciwprostokątnej
1)
W ΔADC:
|AC|2=82+62
|AC|=10
α=60o, |DE|=x −wysokość ΔADC poprowadzona do przeciwprostokątnej
1)
W ΔADC:
|AC|2=82+62
|AC|=10