Twierdzenie Pitagorasa w przestrzeni MarciN888: witam mam problem z tymi zadaniami i mam wielką prośbę o pomoc Twierdzenie Pitagorasa w przestrzeni : 1) Oblicz objętość ostrosłupa prawidłowego trójkątnego , w którym krawędż boczna ma długość 4 dm i jest nachylona do podstawy pod kątem 45 stopni 2) Podstawą graniastosłupa prostego jest romb o przekontnych długości 6cm i 8cm . Dłuższa przekątna graniastosłupa jest nachylona do podstawy pod kątem 60 stopni. Oblicz pole powierzchni całkowitej o objętości tego graniastosłupa ! 3) Przekrój graniastosłupa prawidłowego trójkątnego płaszczyzną , zawierają równoległe wysokości podstaw graniastosłupa , jest kwadratem o przekątnej długości 3√6 dm . oblicz pole powierzchni całkowitej i objętości tego graniastosłupa .

Basia: Rysuję; to potrwa

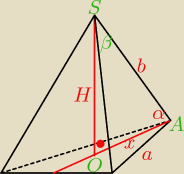Basia: b=4 α=45 podstawą ostrosłupa prawidłowego trójkątnego jest trójkąt równoboczny spodek wysokości H jest środkiem ciężkości podstawy czyli punktem przecięcia wysokości h stąd mamy: tr.AOS jest prostokątny równoramienny bo α+β+90=180 β=180−90−45=45 czyli H=x z tw.Pitagorasa H²+x²=b² H²+H²=4² 2H²=16 H²=8 H=√8=√4*2=2√2 x=2√2 x = ²₃h 2√2=²₃h

	2*3√2
h =		= 3√2
	2

	a√3
h =
	2

	a√3
3√2=
	2

a√3 = 6√2

	6√2		6√6
a=		=		= 2√6
	√3		3

	a2√3		4*6
Pp =		=		= 6
	4		4

	6*2√2
V = 13Pp*H =		=4√2
	3

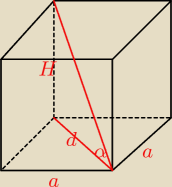Basia: α=60 d=8 e=6

	H
tgα=
	d

	H
tg60=
	8

H = 8*tg60=8√3

	d*e		8*6
Pp =		=		= 24
	2		2

V=P_p*H = 24*8√3 = 192√3 P_c = 2*P_p + 4*a*H przekątne rombu przecinają się w połowie i pod kątem prostym a²=(^d₂)²+(^e₂)² a² = 4²+3² a²=16+9=25 a=5 P_c=48+4*5*8√3 = 48+160√3

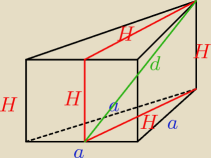Basia: d=3√6 d²=H²+H²=2H² 2H² = 9*6=54 H² = 27 H=√27=√9*3=3√3 h=H=3√3

	a√3
h=
	2

a√3
	=3√3
2

	3√3*2
a =		= 6
	√3

	a2√3		36√3
Pp =		=		= 9√3
	4		4

V=P_p*H = 9√3*3√3 = 27*3=81 P_c = 2*P_p+3*a*H = 18√3+3*6*3√3 = 18√3+3*18√3 = 4*18√3 = 72√3

sdfssfd: δ∞≤≤≤≤≤∞∞∞Ωas dawbwb Ωf fsdh≤ gdh

123: oblicz objetisc ostroslua prawidlowego czworokontnego jesli krawec boczna ma dlugosc 6 cm i tworzy wysoksc ostroslupa 30 stopni