Z talii 24 kart (do gry np. w tysiąca), wyciągnięto losowo 2 karty. KubaAM: Z talii 24 kart (do gry np. w tysiąca), wyciągnięto losowo 2 karty. Niech X oznacza liczbę wylosowanych asów. Znajdź funkcję prawdopodobieństwa, wartość oczekiwaną i odchylenie standardowe zmiennej losowej X.

sushi: ile mozesz wylosować asów ?

KubaAM: 0 lub 1 lub 2, tak?

sushi: tak, to masz X₁, X₂, X₃ teraz trzeba policzyć p₁, p₂, p₃ i masz rozkład dyskretny

KubaAM: schematem bernoulliego to policzę?

sushi: masz karty więc kombinacje

KubaAM: W jaki sposób tę kombinacje stworzyc?

Mila:

	24 2		1
|Ω|=		=		*24*23}=12*23
			2

X₁− nie wylosowano wylosowano ani jednego asa 24−4=20

	20 2		1   *20*19   2		5*19		95
p(X1)=		=		=		=
	24 2		12*23		6*23		138

X₃− wylosowano 2 asy

	4 2		6		1
P(X3)=		=		=
	12*23		12*23		2*23

X₂− wylosowano jednego asa

	95		1		95+3		98		40		20
P(X2)=1−(		+		)=1−		=1−		=		=
	138		46		138		138		138		69

X₁ X₂ X₃ ==================== 0 1 2

	95		20		1
	138		69		2*23

==========================

	95		20		1		1
E(x)=0*		+1*		+2*		=
	138		69		2*23		23

posprawdzaj rachunki i licz odchylenie standardowe

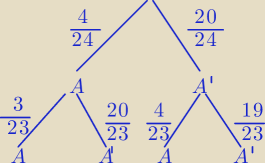
Mila: Jeżeli nie umiesz zastosować wzoru na kombinacje, to licz z drzewka.

	20		19		5*19
P(X1)=P(A'A')=		*		=
	24		23		6*23

itd