trójkąt dominika: dany jest trójkąt o wierzchołkach (2,−1) (4,2) (5,1) wyznacz: a. jego pole b. równanie prostej zawierającej wysokość poprowadzoną z wierzchołka A

Pati: b) a(2, −1) s− środek BC b(4,2) c(5,1)

	4+5		1		1
s(		, {2+1}{2})= (4		, 1		)
	2		2		2

prosta przechodzi przez A(2,−1) i środek boku BC

	(x−x1)(y2−y1)
y−y1=
	(x2−x1)

	3   (x−2)( +1)   2
y+1=
	9   −2 2

i wystarczy obliczyć

Pati: co do punktu a jest wzór na pole trojkąta danego we wspołrzędnych wysokość to AS a podstawa CB

dominika: wychodzi mi cos takiego: P = ¹₂| (4−2)(1+1) − (2+1) (5−2)= ¹₂| 2*2 − 3*3= ¹₂|4 − 9 = −2,5?! czy cos po prostu przeoczyłam dlatego wychodzi wyniku ujemny?

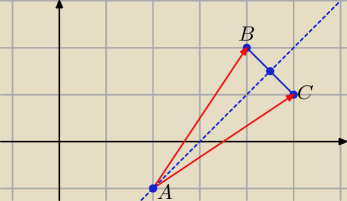Bogdan: A(2, −1), B(4, 2), C(5, 1) → AB = [2, 3] → AC = [3, 2] | 2 3 | Pole P = 0,5* | | | | = 0,5*|4 − 9| = 2,5 | 3 2 | Prosta y = ax + b zawierająca wysokość wychodzącą z wierzchołka A jest prostopadła do prostej y = a_Ax + b_A zawierającej wierzchołki BC, której współczynnik kierunkowy a_A = {1 − 2}{5 − 1+ = −1. Stąd a = 1 oraz y = (x − 2) − 1 ⇒ y = x − 3