Pole obszaru
Zuza: Oblicz pole ograniczonego obszaru zawartego między parabolą x=8−y2 i prostą o równaniu
y=12 x.
Mam rysunek, wyznaczyłam punkty w których wykresy się przecinają, już piszę z czym nie mogę
sobie poradzić: chcę liczyć całki po dy, nie dx, w związku z tym pierwsza całka oznaczona
byłaby od −4 do 0 ∫(2y−8+y2)dy. Druga całka byłaby od 0 do 2 i tu pytanie: odejmuję od
funkcji 8−y2 tę drugą, czy na odwrót?
A może przedstawiony początek rozwiązania jest kompletnie niepoprawny?
10 cze 12:40
Lech: Zrob rysunek dla lini : y = √8−x oraz y =x/2 , wyznacz punkt przeciecia tych lini K(a,b)
i bedziesz mial granice calkowania dla zmiennej x , beda dwa obszary
P = ∫ x/2 dx + ∫ √x−8 dx
pierwsza calka od 0 do a , druga od a do 8
10 cze 12:47
piotr: ∫−42(8 − 2 y − y2)dx = 36
10 cze 13:02
piotr:
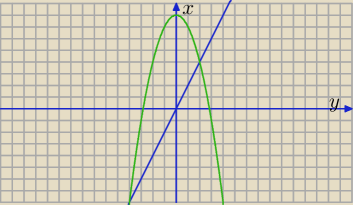
10 cze 13:07
Zuza: A dlaczego odrzucamy możliwość, że y= −√8−x ?
10 cze 13:18
piotr: Licząc całkę po dx:
∫−84 (x/2−(−√8−x))dx + ∫48 (√8−x−(−√8−x))dx
10 cze 13:38
Lech:
Kolego @piotr w Twoim wpisie o g.13.02 powinno byc dy !
10 cze 13:50
piotr: oczywiście Lechu: dy
10 cze 14:22
Zuza: Dziękuję za pomoc!
10 cze 16:45
