szereg geometryczny poziomka: W kwadrat o boku długości a wpisano koło, w które wpisano kwadrat, a w ten kwadrat znów koło itd. Oblicz sumę: a) obwodów b) pól wszystkich kół.

the foxi:

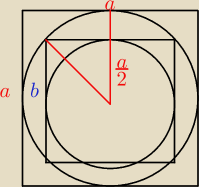
	a
promien koła1:
	2

a
	jest połową przekątnej kwadratu o boku b wpisanego w koło1
2

a		b√2		a√2
	=		⇒ b=
2		2		2

	a√2		a		√2
promien koła2:		=		*
	4		2		2

	a√2		√2		a
idąc tym tokiem rozumowania, promień koła3:		*		=
	4		2		4

	a
kolejne promienie tworzą ciąg geometryczny o pierwszym wyrazie a1=		i ilorazie
	2

	1		√2
q=		=		(mamy spełnione |q|<1)
	√2		2

a) obwód koła=2πr obwód koła₁: πa

	πa√2
obwód koła2:
	2

	πa
obwód koła3:
	2

	a1		πa
S=		=		=...
	1−q		√2   1−   2

b)pole koła=πr²

	πa2
pole koła1=
	4

	πa2   4
S=		=...
	√2   1−   2