Kolejna poprawa
Sebastian Porowski: Dzień dobry
Proszę o pomoc w rozwiazaniu zadań z linka ,część jest
Pozaczynana jednak kompletnie nie wiem co robic dalwj.
Wiem ze na poprawię będą te same zadania tylko inne lliczby.
Liczę na waszą pomoc. Link do zadan;
https://zapodaj.net/87d92fc2cd5e9.jpg.html
9 cze 06:10
PW: A no pewnie. Nie chciało się obrócić obrazka, a ja mam łbem kręcić?
9 cze 12:29
Sebastian Porowski: Przepraszam za sposób wrzucenia zdjęcia w telefonie wszystko było git a niego to wrzucałem
,wysyłam poprawnie
ustawione zdjecie. Jeszcze raz prosze o pomoc z tymi zadaniami. Link do poprawnie ustawionego
zdjęcia :
https://zapodaj.net/27fc2e8e64fdc.jpg.html
9 cze 18:30
iteRacj@:
wpisując treść zadania zwiększasz szanse na otrzymanie odpowiedzi

9 cze 18:34
Mila:
(5,6,7) przepisz, rysunkowe pomogę po 20.
Też mi sprawia kłopot ciągłę zaglądanie do linka.
9 cze 18:39
Sebastian Porowski: już podaje treść zadań :
zad 5 pole rombu wynosi 6 a jedna z przekatnych ma dlugosc 4
oblicz dlugoc boku i wysokosc tego rombu
zad 6 dany jest trojkat prostokatny abc w ktorym
alfa = |KAt BAC| i kat |ACB|=90 stopni
oraz |ab| 6pierwiastków z dwóch i oraz |BC|=4 . wyznacz cosinus alfa
zad 7 oblicz pole i dlugosc przekatnej prostokąta o bokach
2pierwiastek z 3 i pierwiastek z 3−1 .
ile wynosi pole kola opisanego na tym prostokącie?
9 cze 20:54
sushi:
zad5. wzór na pole rombu .......
9 cze 21:01
Mila:
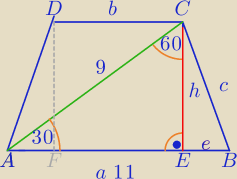
Zadanie 2. Oblicz pole trapezu równoramiennego
1) ΔAECjest połową Δ równobocznego o boku 9.
| | a+b | |
|AE|= |
| ( tak jest w trapezie równoramiennym) |
| | 2 | |
| | 9√3 | |
|AE|= |
| jako wysokość w Δ równobocznym o boku 9. |
| | 2 | |
| | 9√3 | | 9 | | 81√3 | |
PABCD= |
| * |
| = |
| |
| | 2 | | 2 | | 4 | |
=======================
II sposób
1) ΔAECjest połową Δ równobocznego o boku 9.
2) |EB|=e
a=b+2e⇔11=b+2e
| | 9√3 | |
|AE|= |
| jako wysokość w Δ równobocznym o boku 9 |
| | 2 | |
e=11−4.5
√3
⇔11=b+2*(11−4.5
√3)⇔11=b+22−9
√3
b=9
√3−11
3)
============
9 cze 21:08
Mila:
W zadaniu (2) w następnym trapezie liczysz pole z wzoru
| | d1*d2 | |
P= |
| bo przekątne są prostopadłe |
| | 2 | |
albo
Zliczasz pola 4 trójkątów prostokątnych.
Oblicz i podaj wynik. Sprawdzę.
9 cze 21:11
Sebastian Porowski: w 5 bedzie 4*f/2 =6 /mnoze razy 2 wszystko
4f=12 /4
f=3 ?
wiec wysokosc to 1,5
a bok ma dlugosc 4 ?
9 cze 21:16
sushi:
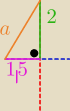
i Pitagoras −−>a =...
potem wzór na pole i masz "h"
9 cze 21:19
Sebastian Porowski: drugi przyklad z trapezem
6*6/2 =18 jako dlugosci przekatnych przyjałęm 6
9 cze 21:20
Sebastian Porowski: Sushi to bedzie 2,25 +4 =6,25
wiec a =2,5?
9 cze 21:23
sushi:
tak, a= 2,5
9 cze 21:24
Mila:
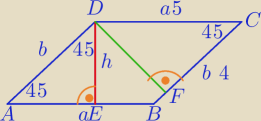
Zadanie 3.
Oblicz pole równoległoboku i obie wysokości, dane na rysunku.
Nie wiem jaki masz przerobiony materiał, która klasa?
Funkcje trygonometryczne były?
1)
ΔAED− Δprostokątny równoramienny
|AE|=h
h
2+h
2=b
2
2h
2=4
2⇔2h
2=16 ⇔h
2=8
h=
√8=
√4*2=2
√2
P
ABCD=5*2
√2=10
√2
II sposób
| | √2 | |
PABCD=a*b*sin(45o)=5*4* |
| |
| | 2 | |
P
ABCD=10
√2
============
2) wysokości, jedna jest h
a=2
√2
P
ABCD=b*h
b
10
√2=4*h
b /:4
==============
9 cze 21:25
Mila:
21:20 dobrze. P=18
9 cze 21:26
Sebastian Porowski: Jestem na poziomie pierwszej klasy,przerabialiśmy funkcje trygonometryczne,jednak jestem z nich
kiepski.
9 cze 21:27
Sebastian Porowski: Czy mógłby ktoś mi doradzić jak wykonać zadanie pierwsze podpunkt a ?
9 cze 21:39
sushi:
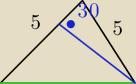
i jest taki wzór
9 cze 21:42
Mila:
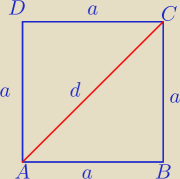
No to trzeba się poduczyć. Masz tam dane na ogół trójkąty ekierkowe, to znasz z Gimnazjum.
W (4) nie wiem co dane w (a, b, c ) a co Ty obliczyłeś,
d) kwadrat.
d=7− długość przekątnej
Mamy dwa sposoby;
1)d=a
√2 − wzór na przekątna kwadratu
7=a
√2 /*
√2
7*
√2=2a
2a=7
√2
Obw
□=4*a
Obw
□=2*2a=14
√2
===========
albo
2)
d
2=a
2+a
a
7
2=2a
2, 49=2a
2
========================
9 cze 21:45
Sebastian Porowski: Sushi dzięki za pomoc, ogarniam wzory na podstawie których to wszystko się wylicza . Mila
oczywiście to wszystko analizuje
wielkie dzięki za pomoc.
9 cze 22:33
Mila:
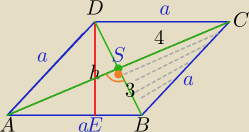
zad 5.
Pole rombu wynosi 6 a jedna z przekątnych ma dlugość 4 .
Oblicz długość boku i wysokość tego rombu.
1)
12=4*p
2
p2=3
2) Przekątne są prostopadłe i dzielą się na połowy:
W ΔBSC: a
2=2
2+(1.5)
2
a
2=4+2.25=6.25
a=2.5
3)
6=2.5*h
==========
9 cze 23:01
Mila:
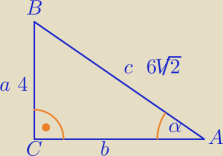
6)
1) c
2=a
2+b
2
(6
√2)
2=4
2+b
2
72−16=b
2
b
2=56=4*14
b=2√14
2)
| | 2√14 | | √14*√2 | |
cosα= |
| = |
| |
| | 6√2 | | 3*2 | |
==============
9 cze 23:14
Mila:
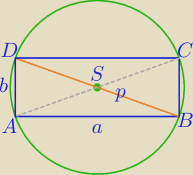
7) Prostokąt
a=2
√3, b=
√3−1
1) Pole prostokąta
P
▭=a*b=2
√3*(
√3−1)
P
▭=2
√3*
√3−2
√3
P
▭=6−2
√3=2*(3−
√3)
2) długość przekątnej:
p
2=(2
√3)
2+(
√3−1)
2
p
2=4*3+3−2
√3+1=16−2
√3
p=
√16−2√3
3) Pole koła opisanego na prostokącie
================
9 cze 23:29
Mila:
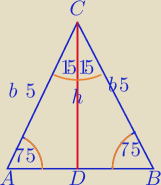
Zadanie 1 a
Znamy kąt między ramionami z sumy kątów w Δ.
| | 1 | |
Możemy pole obliczyc z wzoru P= |
| *b2*sin30o |
| | 2 | |
===========
9 cze 23:39

 Zadanie 2. Oblicz pole trapezu równoramiennego
Zadanie 2. Oblicz pole trapezu równoramiennego
 i Pitagoras −−>a =...
potem wzór na pole i masz "h"
i Pitagoras −−>a =...
potem wzór na pole i masz "h"
 Zadanie 3.
Oblicz pole równoległoboku i obie wysokości, dane na rysunku.
Nie wiem jaki masz przerobiony materiał, która klasa?
Funkcje trygonometryczne były?
1)
ΔAED− Δprostokątny równoramienny
|AE|=h
h2+h2=b2
2h2=42⇔2h2=16 ⇔h2=8
h=√8=√4*2=2√2
PABCD=5*2√2=10√2
II sposób
Zadanie 3.
Oblicz pole równoległoboku i obie wysokości, dane na rysunku.
Nie wiem jaki masz przerobiony materiał, która klasa?
Funkcje trygonometryczne były?
1)
ΔAED− Δprostokątny równoramienny
|AE|=h
h2+h2=b2
2h2=42⇔2h2=16 ⇔h2=8
h=√8=√4*2=2√2
PABCD=5*2√2=10√2
II sposób
 i jest taki wzór
i jest taki wzór
 No to trzeba się poduczyć. Masz tam dane na ogół trójkąty ekierkowe, to znasz z Gimnazjum.
W (4) nie wiem co dane w (a, b, c ) a co Ty obliczyłeś,
d) kwadrat.
d=7− długość przekątnej
Mamy dwa sposoby;
1)d=a√2 − wzór na przekątna kwadratu
7=a√2 /*√2
7*√2=2a
2a=7√2
Obw□=4*a
Obw□=2*2a=14√2
===========
albo
2)
d2=a2+aa
72=2a2, 49=2a2
No to trzeba się poduczyć. Masz tam dane na ogół trójkąty ekierkowe, to znasz z Gimnazjum.
W (4) nie wiem co dane w (a, b, c ) a co Ty obliczyłeś,
d) kwadrat.
d=7− długość przekątnej
Mamy dwa sposoby;
1)d=a√2 − wzór na przekątna kwadratu
7=a√2 /*√2
7*√2=2a
2a=7√2
Obw□=4*a
Obw□=2*2a=14√2
===========
albo
2)
d2=a2+aa
72=2a2, 49=2a2
 zad 5.
Pole rombu wynosi 6 a jedna z przekątnych ma dlugość 4 .
Oblicz długość boku i wysokość tego rombu.
1)
zad 5.
Pole rombu wynosi 6 a jedna z przekątnych ma dlugość 4 .
Oblicz długość boku i wysokość tego rombu.
1)
 6)
6)
 7) Prostokąt
a=2√3, b=√3−1
1) Pole prostokąta
P▭=a*b=2√3*(√3−1)
P▭=2√3*√3−2√3
P▭=6−2√3=2*(3−√3)
2) długość przekątnej:
p2=(2√3)2+(√3−1)2
p2=4*3+3−2√3+1=16−2√3
p=√16−2√3
3) Pole koła opisanego na prostokącie
7) Prostokąt
a=2√3, b=√3−1
1) Pole prostokąta
P▭=a*b=2√3*(√3−1)
P▭=2√3*√3−2√3
P▭=6−2√3=2*(3−√3)
2) długość przekątnej:
p2=(2√3)2+(√3−1)2
p2=4*3+3−2√3+1=16−2√3
p=√16−2√3
3) Pole koła opisanego na prostokącie
 Zadanie 1 a
Zadanie 1 a