drzewa grac: Czy ktoś mógłby mi powiedzieć czym są drzewa samodopełniające? Jak zrobić zadanie 4? http://wmii.uwm.edu.pl/~doliwa/zad-MD-I-11.pdf

Pytający: Drzewo samodopełniające to drzewo, które jest grafem samodopełniającym. Znaczy się drzewo, które jest izomorficzne ze swoim dopełnieniem. Tu masz rozwiązanie: https://math.stackexchange.com/a/369238

grac: Mógłby ktoś narysować to?

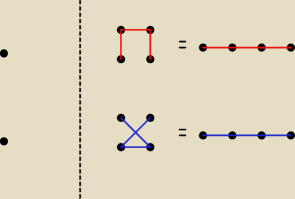
Pytający: Masz drzewa samodopełniające dla n=1 i dla n=4. Dolne jest dopełnieniem górnego i na odwrót. Dla n=4 masz jeszcze te same drzewa narysowane inaczej, coby było widać izometryczność.

grac: "Graf samodopełniający musi mieć połowę krawędzi grafu pełnego o tej samej liczbie wierzchołków. Należy to połączyć z warunkiem łączącym liczbę wierzchołków i krawędzi w drzewie. Dostaniemy stąd ile wierzchołków może mieć takie drzewo. Spośród drzew o takiej liczbie wierzchołków należy wybrać samodopełniające." Jak mam połączyć te warunki? Graf pełny o 8 wierzchołkach ma 28 krawędzi W drzewie liczba krawędzi grafu o 8 wierzchołkach wynosi 7

Pytający: A skąd 8 wierzchołków? W podesłanym wcześniej linku masz napisaną równość (w nieco innej formie), która musi zachodzić dla drzewa samodopełniającego, i która wynika z tego, co właśnie napisałeś:

n 2
	=n−1
2

grac: Zobacz zadanie 4 w linku, który podałem. Tam drzewo ma 8 wierzchołków I muszę do niego wyznaczyć samodoełniające. Ono ma 8wierzchołków więc samodopełniające do niego jak będą wyglądały?

Pytający: Przeczytaj jeszcze raz: treść zadania 4 i treść zadania 5. Rysunek jest do zadania 5. I zgadzam się, nie jest to zbyt przejrzyście przedstawione.

grac: A dobra to moje niedopatrzenie, a ja cały czas szukałem rozwiązania drzewa dopełniającego tych drzew. Więc co będzie odpowiedzią do tego zadania? Drzewa dla n=1 i 4 tylko?

Pytający: Tak, ale musisz je narysować, bo dla n=4 są dwa różne drzewa ze względu na izomorfizm (patrz rysunek), ale tylko pierwsze z nich jest drzewem samodopełniającym (co rysowałem wyżej). Dopełnienie drugiego nawet nie jest drzewem (więc nie ma mowy o izomorfizmie). I wyżej pisałem o izometryczności, a nie o izomorfizmie... coś mi się pogmatwało.

grac: Dzięki za pomoc