| AD | sin(α+2β) | |||
β. Wykaż, że: | = | , gdzie 180 stopni<α+2β<360 stopni i 0 | ||
| DB | −sinα |

 z.
0<α+2β<360 i 0<α+β<180
1)
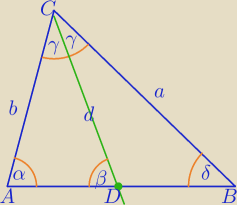
α+β+γ=180
α+δ+2γ=180⇔δ=α+2β−180
2)
Z twierdzenia o dwusiecznej kąta ACB w ΔABC:
z.
0<α+2β<360 i 0<α+β<180
1)
α+β+γ=180
α+δ+2γ=180⇔δ=α+2β−180
2)
Z twierdzenia o dwusiecznej kąta ACB w ΔABC:
| b | AD | ||
= | |||
| a | DB |
| b | a | ||
= | ⇔ | ||
| sinδ | sinα |
| b | sinδ | sin((α+2β)−180) | −sin(180−(α+2β)) | ||||
= | = | = | = | ||||
| a | sinα | sinα | sinα |
| −sin(α+2β) | AD | |||
= | = | |||
| sinα | DB |