Geometria analityczna zadanie Uczeń: Punkty P=(−2,−1) i Q=(3,2) są przeciwległymi wierzchołkami kwadratu. Napisz równanie okręgu opisanego na tym kwadracie.

sushi: znajdź środek odcinka PQ −−> to będzie środek okręgu policz długość odcinka |PQ| −−> potem jego połowa = promień szukanego okręgu

Mila: P=(−2,−1) , Q=(3,2)

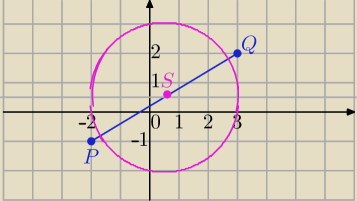
	−2+3		−1+2
S=(		,		)⇔
	2		2

	1		1
S=(		,		) współrzędne środka okręgu
	2		2

	26
|SQ|2=R2=(3−1/2)2+(2−1/2)2=
	4

Równanie okręgu:

	1		1		26
(x−		)2+(y−		)2=
	2		2		4

====================

an:

17
2

a7:

13
2

jest dobrze ( i bardzo elegancko)