Okrąg P: Dane są okręgi o środkach A, B, C i promieniach równych odpowiednio r, 2r,3r. Każde dwa z tych okręgów są zewnętrznie styczne: pierwszy z drugim w punkcie K, drugi z trzecim w punkcie L i trzeci z pierwszym w punkcie M. Oblicz stosunek pola trójkąta KLM do pola trójkąta ABC.

Eta: 1/5

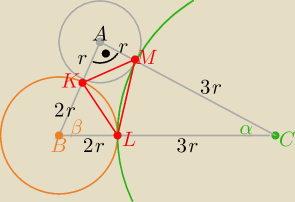
Eta: Trójkąt ABC ma wymiary : 3r,4r,5r zatem jest prostokątny

	1
P(ABC)=		*3r*4r=6r2
	2

	1		1
P(KAM)=		*r*r=		r2
	2		2

sinα=3/5 , sinβ=4/5

	1
P(KBL)=		*2r*2r*sinβ=..........
	2

	1
P(MLC)=		*3r*3r*sinα=.................
	2

teraz od P(ABC) odejmij sumę pól P(KAM)+P(MLC)+P(KBL)=........ otrzymasz pole P(KLM)=......... i dokończ.....................

P: Ok

Eta: