Trójkat
Witek: W trójkącie równobocznym ABC na boku BC obrano taki punt P, że |BP| : |PC| = 1:2. Oblicz
tangens kąta PAB.
6 cze 12:16
Blee:
1) z tw. Cosinusow wyznaczasz dlugosc |AP|
2) majac dlugosci trojkata ABP wyznaczasz cosinusa szukanego kata
3) z jedynki trygonometrycznej wyznaczasz sinusa tegoz kata
4) majac sinusa i cosinusa wyznaczasz tangensa
6 cze 12:45
Witek: Trochę skomplikowane, możesz zacząć ?
6 cze 13:48
Blee:
1) x
2 = (3a)
2 + a
2 − 2*3a*a*cos(60
o)
Czyli x =
√7a
2) a
2 = 7a
2 + 9a
2 − 6
√7a
2cosα
4) tgα = sinα/cosα = ...
6 cze 14:09
6 cze 14:17
Blee:
Skroc √7 bo w koncu √21 = √3*√7
6 cze 14:18
Blee:
Co zauwazysz jezeli to na spokojnie przeliczysz
6 cze 14:19
6 cze 14:28
Blee:
Da
Ale obliczenia sam zrob i sprawdz czy sie gdzies nie jebnalem.
6 cze 14:30
Eta:
==========
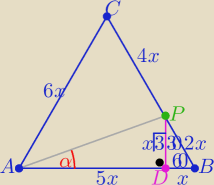i po "ptokach"
6 cze 15:42
Witek: Dzieki wielkie !
6 cze 16:10
Mila:
Lubelska próba przed maturą− klasa I.
6 cze 18:18
