ekstremum lokalne maja:

	x3−2x+4
f(x)=		, Df = R\{2}
	x−2

	2x2(x−3)
f'(x)=
	(x−2)2

f'(x)>0 ⇔ x ∊ (−∞,0 ) (3,∞) f'(x)<0 ⇔ x ∊(0,3) f'(x)=0 ⇔ x =0 x =3 f(0 ) = −2−min a f(3) = 25 −maks w odpowiedzi mam że minimum mam w x=3 dlaczego?

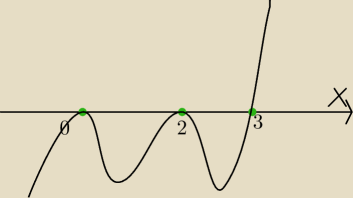
the foxi: f'(x)<0 ⇔ 2x²(x−3)(x−2)²<0 w x=0 nie mamy ekstremum a w x=3 jest minimum, ponieważ pochodna zmienia znak z minus na plus.

the foxi: w x=2 powinna być pusta kropka

the foxi: nie możesz patrzeć, która wartość − f(0) czy f(3) jest większa i na podstawie tego decydować o rodzaju ekstremum

maja: nie rozumiem. przecież na lewo od x = 0 rośnie a później maleje? więc powinno być maksimum?

the foxi: maksimum jest wtedy, gdy pochodna dla pewnego x₀ przyjmuje wartość zero, a "na lewo" od niej była ujemna, a "za nią" jest dodatnia krótko mówiąc, max jest wtedy, gdy pochodna przechodzi przez oś iksów i z dodatniej jest ujemna analogicznie z minimum

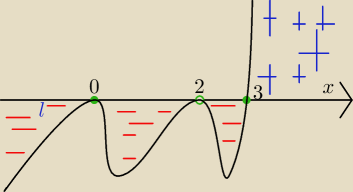
the foxi: chyba lepiej wyjaśnione koślawe te plusy, ale mniejsza tam, gdzie pochodna jest ujemna (od −∞ do 3), funkcja maleje tam, gdzie jest dodatnia (od 3 do +∞), tam rośnie w punkcie x=3 pochodnia przechodzi z minusów na plus więc to oznacza, że mamy minumum