Wprowadzając współrzędne biegunowe obliczyć całkę (naszkicować obszary całkowani Karkon: Całka podwójna po obszarze D (xdxdy) gdzie obszar D ograniczają okręgi x²+y²=4y, x²+y²=4√3x. Wiem jak policzyć jak jest jedno koło, ale jak to policzyć jak są 2?

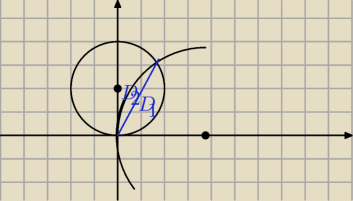
Basia: masz: x²+y²−4y=0 x²+(y−2)²−4=0 x²+(y−2)²=4 S₁=(0;2) r₁=2 x²+y²−4√3x=0 (x−2√3)²−12+y²=0 (x−2√3)²+y²=12 S₂=(2√3;0) r₂=2√3 Twój obszar całkowania to część wspólna tych kół szukasz punktów wspólnych okręgów to będą A=(0;0) i B=(√3;3) i dzielisz obszar całkowania na dwa prostą AB

	3
ona ma współczynnik kierunkowy a=		=√3
	√3

	π
czyli tg α = √3 czyli α =
	3

	π
więc obszar D1 masz ograniczony przez: 0≤φ≤
	3

i okrąg x²+y²=4y r²cos² φ + r²sin² φ = 4rsin φ r² − 4rsin φ =0 r(r−4sin φ)=0 r=4sin φ 0 ≤ r ≤ 4sin φ i na obszarsze D₁ masz ₀∫^π/3 dφ ₀∫^{4sin φ} r²cos φ dr

	π		π
obszar D2 masz ograniczony przez:		≤ φ ≤
	3		2

i okrąg x²+y²=4√3x r²cos² φ + r²sin² φ = 4√3rcos φ r² − 4√3rcos φ = 0 r(r−4√3cos φ)=0 r = 4√3cos φ i na obszarze D₂ masz _π/3∫^π/2 dφ ₀∫^{4√3cos φ} r²cos φ dr