 2x+2y=48 ⇒ x+y=24 ⇒y=24−x, x∊(0;24)
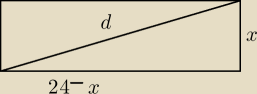
oznaczmy przekątną jako d
x2+(24−x)2=d2
x2+576−48x+x2=d2
d2=2x2−48x+576
d=√2x2−48x+576
i liczysz minimum funkcji d(x)=√2x2−48x+576
a tak na marginesie, można się domyślić, że przekątna najkrótsza będzie dla kwadratu, czyli
x=12, ale ciii..
2x+2y=48 ⇒ x+y=24 ⇒y=24−x, x∊(0;24)
oznaczmy przekątną jako d
x2+(24−x)2=d2
x2+576−48x+x2=d2
d2=2x2−48x+576
d=√2x2−48x+576
i liczysz minimum funkcji d(x)=√2x2−48x+576
a tak na marginesie, można się domyślić, że przekątna najkrótsza będzie dla kwadratu, czyli
x=12, ale ciii.. 
 Trochę się pogubiłam w moich przekształceniach, ale już się odnalazłam. Dziękuję bardzo!
Trochę się pogubiłam w moich przekształceniach, ale już się odnalazłam. Dziękuję bardzo!
| (x+y)2 + (x−y)2 | (x + y)2 | |||
x2 + y2 = | ≥ | = 24*12 | ||
| 2 | 2 |