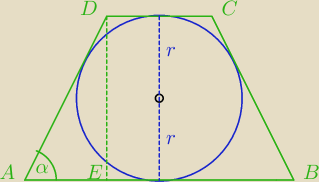
x x: Na kole o promieniu długości 4√3 opisano trapez równoramienny. Jaką miarę musi mieć kąt ostry trapezu, aby jego pole było najmniejsze?

iteRacj@: 0^o<α<90^o |DE|=2r=8√3

	1
PABCD=		(|AB|+|DC|)*|DE|
	2

|AB|+|DC|=|AD|+|BC| − czworokąt opisany na okręgu

	1
PABCD=		(|AD|+|BC|)*8√3
	2

	|DE|
sin α=
	|AD|

	8√3
|AD|=|BC|=
	sin α

	8√3		64*3
PABCD=(2*		)*4√3=
	sin α		sin α

i teraz pytanie, kiedy to pole będzie najmniejsze?

Eta: h=2r i a+b=2c i c=2r/sinα

	4r2
P=2cr ⇒ P(α)=
	sinα

pole jest najmniejsze gdy sinα=1 ⇒ α=90^o zatem takim trapezem jest kwadrat o boku 2r dla r=4√3 najmniejsze pole : P=4r²=192 [j²] ============