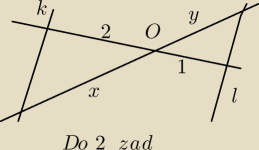 1. Cięciwa okręgu ma długość 24cm. Środek tego okręgu znajduje się w odległości 5cm od tej
cięciwy.
Oblicz długość średnicy
2. Na rysunku obok proste k i l są równoległe oraz dane są długości odcinków wyznaczonych przez
punkt O i te proste.
Wyznacz x jeżeli x+y=6 (do tego jest rysunek)
3.w trójkącie prostokątnym jedna przyprostokątna jest o 3cm krótsza od przeciwprostokątnej.
Druga
przyprostokątna ma długość 9cm. Oblicz:
a) obwód trójkąta
b)długość promienia okręgu opisanego na tym trójkącie
c) długość promienia okręgu wpisanego w ten trójkąt
d) odległość punktu przecięcia środkowych trójkąta od wierzchołka kąta prostego
4. W trójkącie równoramiennym ABC mamy |AC| = |BC|. Wysokość AD podzieliła ramię BC na
odcinki długości:
|BD|=3cm, |DC|=7cm Oblicz:
A) dłguość podstawy AB
b) długość wszystkich wysokości tego trójkąta.
5y. odcinek AB ma długość 8cm. Na symetralnej k odcinka AB, w odległości 6cm od tego odcinka
zaznaczono punkt C. W takiej odległości od środka odcinka AB należy przeprowadzić prostą l
równoległą do prostej k, aby punkty przecięcia prostej l z odcinkami AB i AC wyznaczyły odcinek
długości 4cm? Wykonaj odpowiedni rysunek do tego zadania.
1. Cięciwa okręgu ma długość 24cm. Środek tego okręgu znajduje się w odległości 5cm od tej
cięciwy.
Oblicz długość średnicy
2. Na rysunku obok proste k i l są równoległe oraz dane są długości odcinków wyznaczonych przez
punkt O i te proste.
Wyznacz x jeżeli x+y=6 (do tego jest rysunek)
3.w trójkącie prostokątnym jedna przyprostokątna jest o 3cm krótsza od przeciwprostokątnej.
Druga
przyprostokątna ma długość 9cm. Oblicz:
a) obwód trójkąta
b)długość promienia okręgu opisanego na tym trójkącie
c) długość promienia okręgu wpisanego w ten trójkąt
d) odległość punktu przecięcia środkowych trójkąta od wierzchołka kąta prostego
4. W trójkącie równoramiennym ABC mamy |AC| = |BC|. Wysokość AD podzieliła ramię BC na
odcinki długości:
|BD|=3cm, |DC|=7cm Oblicz:
A) dłguość podstawy AB
b) długość wszystkich wysokości tego trójkąta.
5y. odcinek AB ma długość 8cm. Na symetralnej k odcinka AB, w odległości 6cm od tego odcinka
zaznaczono punkt C. W takiej odległości od środka odcinka AB należy przeprowadzić prostą l
równoległą do prostej k, aby punkty przecięcia prostej l z odcinkami AB i AC wyznaczyły odcinek
długości 4cm? Wykonaj odpowiedni rysunek do tego zadania.
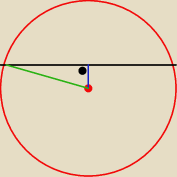 1)
czarna linia to średnica = 24cm
niebieska to odległość od środka okręgu = 5cm (zauważ że jest pod kątem prostym do średnicy i
dzieli ją na pół!)
zielona linia − promień okręgu
Pitagoras i lecisz
1)
czarna linia to średnica = 24cm
niebieska to odległość od środka okręgu = 5cm (zauważ że jest pod kątem prostym do średnicy i
dzieli ją na pół!)
zielona linia − promień okręgu
Pitagoras i lecisz
 a niebieska jest pod kątem prostym do cięciwy również*
a niebieska jest pod kątem prostym do cięciwy również*

| y | x | ||
= | ⇒ x=2y | ||
| 1 | 2 |

 Mógłby ktoś mi jeszcze zrobić 3 i 4 przynajmniej? Wtedy już byłbym
w pełni zadowolony
Mógłby ktoś mi jeszcze zrobić 3 i 4 przynajmniej? Wtedy już byłbym
w pełni zadowolony
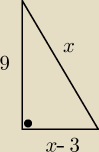 3)
wiesz co z tym zrobić?
3)
wiesz co z tym zrobić? 
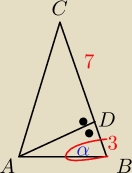 4)
4)

 4) Ja przeciągnąłem wysokość od C do połowy |AB| i tak będzie np. E
Wtedy te dwa odcinki są równe czyli X to wtedy 32x = x10 i to na krzyż
wyjdzie, że podstawa ma 2√15
A w b) dałem wysokość |AD| dałem jak Y To będzie z pitagorasa 32 + 2√152 = y .Jest jak na
razie dobrze?
4) Ja przeciągnąłem wysokość od C do połowy |AB| i tak będzie np. E
Wtedy te dwa odcinki są równe czyli X to wtedy 32x = x10 i to na krzyż
wyjdzie, że podstawa ma 2√15
A w b) dałem wysokość |AD| dałem jak Y To będzie z pitagorasa 32 + 2√152 = y .Jest jak na
razie dobrze?
 proszę niech ktoś inny przejmie temacik
proszę niech ktoś inny przejmie temacik
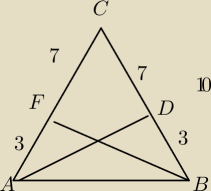 ok ja chyba umiem zrobić zad4
liczymy BF (F wysokość z punktuB) z Pitagorasa
BF2=100−49=51
BF=√51
liczymy podstawę tez z P0itagorasa
AB2=9=51=60
AB=√60
ok ja chyba umiem zrobić zad4
liczymy BF (F wysokość z punktuB) z Pitagorasa
BF2=100−49=51
BF=√51
liczymy podstawę tez z P0itagorasa
AB2=9=51=60
AB=√60
 myślę że dobrze pomyślane z wysokością, ale nie jestem ekspertem od
planimetrii
myślę że dobrze pomyślane z wysokością, ale nie jestem ekspertem od
planimetrii 
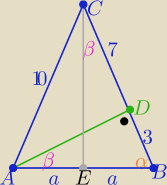 zad.4
Z podobieństwa trójkątów ABD i ABC z cechy (kkk)
zad.4
Z podobieństwa trójkątów ABD i ABC z cechy (kkk)
| 3 | a | ||
= | ⇒ 2a2=30 /*2 4a2=60 ⇒ 2a=√60 | ||
| 2a | 10 |