mat zs: Z drutu długości 1m zbudowano trójkąt prostokątny o największym polu. Znajdź długości boków tego trójkąta. Wiem, że takie zadanie już tu było, jednak ja mam narzucony sposób rozwiązania: mam układ

	xy
równań x+y+√x2+y2=100 i P=		. Muszę z pierwszego równania wyznaczyć x lub y. Proszę
	2

o pomoc, zupełnie nie wiem jak za to się zabrać!

a7: przekształcamy prze przenisienie x=y na drugą stronę i podniesienie do kwadratu x²+y²=100²−2*100(x+y)+(x+y)² teraz wyliczamy x lub y

a7: miałam na myśli , że x+y przenosimy na drugą stronę, ale widze , że tam zostanie 2x*y

a7: no więc bierzemy y przed nawias i wychodzi y(2x−200)=200x−10000

	200x−10000
y=
	2x−200

a7: y=(100x−5000)/(x−100)

a7: czy dalej już wiesz jak zrobic?

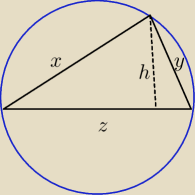PW: Podejście do tego problemu powinno być nieco inne. Podali w treści zadania, że trójkąt ma maksymalne pole. Trójkąt prostokatny o przyprostokątnych długości x, y i przeciwprostokątnej z=√x²+y² jest wpisany w półokrąg − jak na rysunku. Jest zatem oczywiste, że największe pole ma trójkąt o największej wysokości h, czyli trójkąt o równych przyprostokątnych y=x. Wystarczy odpowiedzieć na pytanie, czy istnieje liczba dodatnia x<100, dla której x+x+√x²+x²=100. 2x+√2x=100 (2+√2)x=100

	100
x=		.
	2+√2

Jest to liczba dodatnia i mniejsza od 100, jest więc szukanym rozwiązaniem.

	100
Odpowiedź: Przyprostokątne trójkąta mają równe długości x=		, a przeciwprostokatna
	2+√2

	100		100
ma długość √2		=		.
	2+√2		√2+1