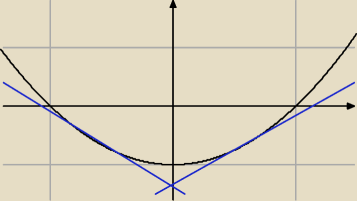
Ostatnie przed maturą matma po nocach: Poprowadzono styczną do paraboli o równaniu y= x² −1 tak, aby trójkąt ograniczony tą styczną i osiami układu współrzędnych miał najmniejsze pole. Oblicz to pole. a=f'(x₀)=2x₀ b=f(x₀)−f'(x₀)x₀=−x₀²−1 y=2x₀x−x₀²−1 to miejsce zerowe będzie dla: 0=2x₀x−x₀²−1

	x02+1
x=
	x0

	x02+1
|x|=		=długość podstawy
	x0

|y|=2x₀x−x₀²−1=wysokość

	x02+1
PΔ=0,5*x*y=0,5*		*(2x0x−x02−1)
	x0

i jestem w kropce, bo mam tego "zwykłego" x i nie wiem co dalej. W kryteriach funkcja

	x04+2x02+1
optymalizowana wynosi P=		więc mając już ten fakt na uwadze widać, że
	4x0

współczynnik przy x₀⁴ przy mojej funkcji będzie inny.

matma po nocach: Okej, podstawiłem do y=2x₀x−x₀²−1 za x=0, dało mi to wysokość w danym trójkącie, czyli y=−x₀²−1.

	x04+2x02+1
P=−		. Mam jednak ten minus, co nie jest możliwe przy obliczaniu pola
	4x0

matma po nocach: Powinienem wziąć do równania moduł z y? Jako, że to wysokość i dla postaci y=−x₀²−1 y nie przyjmuje wartości dodatnich?

Basia: f(x)=x²−1 f'(x) = 2x y=g(x) = 2x₀*x + b x₀²−1 = 2x₀*x₀ + b b = −x₀²−1 y = g(x) = 2x₀*x − x₀²−1 punkt przeciećia z osią OX 2x₀*x −x₀²−1 = 0

	x02+1
x =		// tu zjadłeś liczbę 2
	2x0

punky przecięcia z osią OY // tu za x trzeba podstawić 0 y=g(0) = 2x₀*0 − x₀²−1 = −x₀²−1

	x02+1
a = |x| =
	2x0

h = |y| = x₀²+1

	1		(x02+1		(x02+1)2		x+04+2x+02+1
P =		*		(x02+1} =		=
	2		2x0		4x0		4x0

	x4+2x2+1
P(x) =
	4x

matma po nocach: Świetnie, pięknie dziękuję za pomoc

Basia: co do a................ powinno zasadniczo być

	x02+1
a =
	|x0|

możemy sobie albo: 1. założyć, że x₀>0 i pamietać, że będą dwie proste spełniające warunki zadania; one i tak wyjdą z rozwiązania, ale zasadniczo to ujemne należałoby odrzucić i dodać z powrotem z uzasadnieniem (osią symetrii paraboli jest OY, styczne spełniające warunki zadania są symetryczne względem OY) 2. rozważać dwie funkcje

	x4+2x2+1
P(x) =		dla x>0
	4x

lub

	x4+2x2+1
P(x) =		dla x<0
	−4x

trochę szkoda czasu, ale gdyby to była inna parabola mogłoby już nie być tak dobrze

Basia:

	x02+1
a =		oczywiście
	2|x0|

Basia: albo jeszcze prościej zakładamy, że x>0

	1		x02+1
szukane pole =		pola trójkąta o podstawie 2x =		i wysokości |y|=x02+1
	2		x0

właśnie dlatego, że styczne muszą tu być symetryczne względem OY i wszystko jasne

matma po nocach: Wszystko jasne