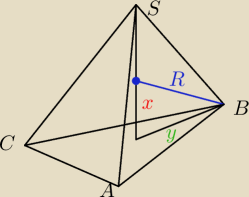
ostrosłup matma po nocach: Na ostrosłupie prawidłowym trójkątnym opisano kulę o promieniu 6. Wykaż, że ten ostrosłup jest czworościanem jeśli wiadomo, że ma objętość największą z możliwych. Oblicz tę objętość.

	2		2		a√3		a√3
y=		h=		*		=
	3		3		2		3

	a√3
x2+(		)2=36 (1)
	3

	1
V=		Pp*H
	3

	a2√3
Pp=
	4

H=R+x=6+x i nie mogę poradzić sobie z funkcją optymalizowaną, mógłby mi ktoś pomóc?

matma po nocach: (1) była do czegoś co pisałem i nie usunąłem

Basia:

	3a2
x2 +		= 36
	9

	a2
x2 +		= 36
	3

	a2
x2 = 36 −
	3

	36*3 − a2		108−a2
x2 =		=
	3		3

	√108−a2
x =
	√3

	1		a2√3		√1−8−a2		1
V =		*		*		=		a2*√108−a2
	3		4		√3		12

	1		1
V' =		*[ 2a*√108−a2 + a2*		*(−2a) ]
	12		2√108−a2

	1		2a*(108−a2) − a3
V' =		*
	12		√108−a2

	1		−3a3+216a
V' =		*
	12		√108−a2

i zajmujesz sie tylko licznikiem czyli wyrażeniem −3a³+216a w przedziale (0; 6√3)

	1
bo wyrażenie		*U{1}{√108−a2 jest stale dodatnie
	12

−3a³+216a = 0 3a(−a²+72)=0 3a>0 −a²+72=0 a² = 72 a = 6√2 i tu masz maksimum musisz teraz jeszcze pokazać, że krawędź boczna też równa się 6√2

matma po nocach: Dziękuję bardzo

Basia: ale coś mi się tutaj nie zgadza; możliwe, że się pomyliłam w rachunkach

Basia: jasne, że tak; od razu przy zapisie V

Basia:

	1		a2√3		√108−a2
V =		*		*(6+		)
	3		4		√3

	1
V =		*[ 6a2√3 + a2√108−a2 ]
	12

	1		1
V' =		* [ 12a√3 + 2a√108−a2 + a2*		*(−2a) ]
	12		2√108−a2

	1		a3
V' =		*[ 12a√3+ 2a√108−a2 −		]
	12		√108−a2

	1		12a√3√108−a2 + 2a(108−a2) − a3
V' =		*[
	12		√108−a2

	1
V' =		*[ 12√3a√108−a2 − 3a3 + 216a]
	12√108−a2

12√3a√108−a² − 3a³ + 216a = 0 3a(4√3√108−a² − a² + 72) = 0 koszmarne to jest, może od innej zmiennej to uzależnić 4√3√108−a² = a²−72 16*3*(108−a²) = a⁴−144a² + 72² 48*108 − 48a² = a⁴−144a² + 72² a⁴ − 96a² + 5184 − 5184 =0 nie takie koszmarne się okazało a²(a²−96)=0 a²=96 a = 4√6

	√108−96		√12
x =		=		= √4 = 2
	√3		√3

	4√6*√3		4√18		4*3√2
y =		=		=		= 4√2
	3		3		3

H = 8 b² = H² + y² b² = 64+16*2 = 64+32 = 96 b = √96 = √16*6 = 4√6 to jest czworościan, ale wykazanie, że dla a=4√6 mamy maksimum nie jest takie proste może naprawdę od innej zmiennej to uzależnić, ale trzeba by popróbować może od x poszłoby latwiej, albo od kąta między y i R

Basia: bardzo ładnie wychodzi z kątem α − kąt między y i x α∊(0^o; 90^o)

	x
sin α =
	6

x = 6*sin α H = 6+6*sin α = 6(1+sin α)

	y
cos α =
	6

y = 6*cos α

a√3
	= 6*cos α
3

a = 6√3*cos α

	1		a2√3		1
V =		*		*H =		*36*3*cos2(α)*6(1+sin α) =
	3		4		12

54(1−sin² α)(1+sin α) = 54(1+sin α − sin² α − sin³ α) sin α ∊ (0;1) t = sin α V=54(−t³−t²+t+1) V' = 54(−3t²−2t+1) −3t²−2t+1=0 Δ=4−4*(−3)*1 = 16 √Δ=4

	2−4		1
t1 =		=
	−6		3

	2+4
t2 =		= −1
	−6

	1
t∊(0;		) ⇒ V'>0 ⇒ V↗
	3

	1
t∊(		;1) ⇒ V'<0 ⇒ V↙
	3

	1
dla t=		funkcja osiąga maksimum
	3

i mamy

	1
sin α =
	3

	2√2
cos α = √1−1/9 = √8/9 =
	3

	2√2
a = 6√3*		= 4√6
	3

	1		4
H = 6(1+		) = 6*		=8
	3		3

	12√2
y =		= 4√2
	3

b² = H²+y² = 64+16*2 = 96 b = √96=√16*6 = 4√6 = a ostrosłup jest czworościanem

	1		1		1		27+9−3−1
Vmax = 54(1+		−		−		) = 54*		= 2*32 = 64
	3		9		27		27

Basia: α kąt między y i R oczywiście, poza tym wszystko dobrze

matma po nocach: Rozwiązania z kątami nawet bym nie brał pod uwagę, a tu proszę, o wiele ładniejsze. Dziękuję

matma po nocach: Uzależniając od x też wychodzą nam ciężkie rachunki, ale jest to nieco ładniejsze, bo usuwa nam się pierwiastek przez wzór na pole trójkąta równobocznego we wzorze na objętość i reszta zgrywa się już w lepszą całość.

Basia: W zadaniach "na styku" stereometrii (także planimetrii) i optymalizacji bardzo często właśnie wprowadzenie kąta daje ładne, proste rozwiązania. Ostatnie zadanie z tegorocznej matury rozszerzonej można tym sposobem szybko rozwiązać. Warto o tym pamiętać