trójkąt piesek50: Długość okręgu wpisanego w trójkąt równoboczny wynosi 6 π. Jaka jest długość boku tego trójkąta?

sushi: wzory znasz ?

a7: 6π=2πr r=3 r=1/3H H=9 P=1/2aH P=1/2a2sinα

	(18√3)
a=
	3

a7: ?

TOSIA: a= 6 √3

trójkąt: 2πr=6π ⇒ r=3 a=2r√3 = 6√3

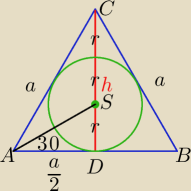
Mila: 1) 2πr=6π r=3 h=3*r=9 I sposób Ze wzoru na wysokość w Δrównobocznycm

	a√3
h=
	2

a√3
	=9
2

a√3=18 /*√3 3a=18√3 a=6√3 II sposób: W ΔADC: z twierdzenia Pitagorasa

	a
a2=(		)2+92
	2

	1
a2=		a2+81
	4

3		4
	a2=81 /*
4		3

a²=108=3*36 a=6√3 albo W ΔADS: |AS|=2r=6

	1		1
62=(		)a2+32⇔		a2=27
	2		4

a²=108 a=6√3 III sposób W ΔADS:

	0.5a
ctg(30o)=
	3

	0.5a
√3=
	3

a=6√3 ===========