Czworokąt wypukły, ciąg arytmetyczny i... Kamila: Mam problem z kilkoma zadaniami. 1. Obwód czworokata wypukłego ABCD jest równy 50cm. Obwód trójkąta ABD jest równy 46cm, a trójkata BCD 36cm. Oblicz długość przekątnej BD. 2. Ile wyrazów ujemnych ma ciąg (a_n) określony wzorem a_n = n² − 2n − 24 dla n ≥ 1? 3. Ile jest liczb naturalnych czterocyfrowych takich, że w ich zapisie dziesiętnym występuje jedna cyfra nieparzysta i trzy cyfry parzyste? Uwaga: zero jest liczbą parzystą.

Kamila: Błagam o pomoc

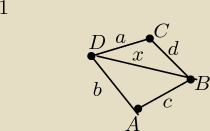
judith: Oznaczyłam długości boków dla skrócenia zapisu: Obwód czworokąta: a+b+c+d=50 Obwód trójkąta ABD: b+c+x=46 , Obwód trójkąta BCD: a+d+x=36 Sumuje obwody trójkątów : b+c+x+a+d+x=46+36 przestawiam wyrazy a+b+c+d+2x=82 ale wiem,że a+b+c+d=50 zatem podstawiam do powyższego równania 50+2x=82, rozwiązuje na jedną stronę wiadome na drugą niewiadomu przenosząc zmieniam znak 2x=82−50, 2x=32, zatem x=18 a x jest równy długości przekątnej BD 2.Należy sprawdzić monotoniczność ciągu ( czy jest rosnący czy malejący) jeżeli a_n+1−a_n>0 to cią rosnący jak a_n+1−a_n<0 to malejący. a_n+1=(n+1)²−2(n+1)−24 ( w miejsce n podstawiłam n+1) a_n+1−a_n=(n+1)²−2(n+1)−24−(n²−2n−24)=2n−1 ale n>=1 więc 2n−1>0 zatem ciąg jest rosnący Sprawdzam teraz dla którego wyrazu ciąg się zeruje n²−2n−24=0. Obliczam delte i pierwiastki. Powinno wyjść n₁=−4 ale n>=1 więc sprzeczność a n₂=6 jest ok. Jeżeli 6 wyraz jest zeram a ciąg jest rosnący zatem wyrazy od 1 do 5 będą mniejsze od zera jest ich 5